题目内容
【题目】若矩形的一条角平分线分一边为3cm和5cm两部分，则矩形的周长为（ ）
A.22B.26C.22或26D.28或26
【答案】C
【解析】
根据平行线的性质，以及角平分线的定义，即可证得∠ABE=∠AEB，利用等角对等边可以证得AB=AE，然后分AE=3cm，DE=5cm和AE=5cm，DE=3cm两种情况即可求得矩形的边长，从而求解．
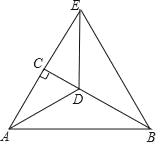
解：如图：∵AD∥BC，
∴∠AEB=∠EBC
又∵BE平分∠ABC，即∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE．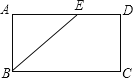
当AE=3cm，DE=5cm时，AD=BC=8cm，AB=CD=AE=3cm．
∴矩形ABCD的周长是：2×8+2×3=22cm；
当AE=5cm，DE=3cm时，AD=BC=8cm，AB=CD=AE=5cm，
∴矩形ABCD的周长是：2×8+2×5=26cm．
故矩形的周长是：22cm或26cm．
故选：C．
练习册系列答案
相关题目
【题目】某校九年级有200名学生，为了向市团委推荐本年级一名学生参加团代会，按如下程序进行了民主投票，推荐的程序如下：首先由全年级学生对六名候选人进行投票，每名学生只能给一名候选人投票，选出票数多的前三名；然后再对这三名候选人（记为甲、乙、丙）进行笔试和面试．两个程序的结果统计如下：
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
请你根据以上信息解答下列问题：
（1）请分别计算甲、乙、丙的得票数；
（2）若规定每名候选人得一票记1分，将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩，成绩最高的将被推荐，请通过计算说明甲、乙、丙哪名学生将被推荐．
