题目内容
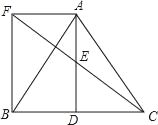
【题目】如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
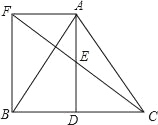
【答案】(1)证明见解析;(2)若AB=AC,则四边形AFBD是矩形.理由见解析.
【解析】分析:(1)因为AF∥BC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有BD=DC;
(2)由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又因为AD=CF,故可根据对角线相等的平行四边形是矩形进行判定.
详解:(1)证明:∵AF∥BC,
∴∠AFE=∠DCE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,
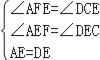 ,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴CD=BD,
∴D是BC的中点;
(2)解:若AB=AC,则四边形AFBD是矩形.理由如下:
∵△AEF≌△DEC,
∴AF=CD,
∵AF=BD,
∴CD=BD;
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.

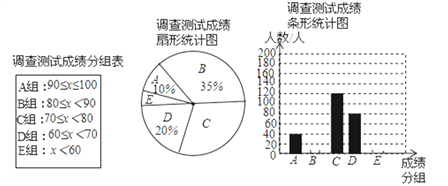
【题目】某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序如下:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试.两个程序的结果统计如下:

测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
【题目】某市近期公布的居民用天然气阶梯价格听证会方案如下:
第一档天然气用量 | 第二档天然气用量 | 第三档天然气用量 |
年用天然气量 | 年用天然气量超出 | 年用天然气量 |
例:若某户![]() 年使用天气然
年使用天气然![]() 立方米,按该方案计算,则需缴纳天然气费为:
立方米,按该方案计算,则需缴纳天然气费为:![]() ×
×![]() +
+![]() ×(
×(![]() -
-![]() )=
)=![]() (元);依此方案请回答:
(元);依此方案请回答:
![]() 若小明家
若小明家![]() 年使用天然气
年使用天然气![]() 立方米,则需缴纳天然气费为_____元(直接写出结果).
立方米,则需缴纳天然气费为_____元(直接写出结果).
![]()
![]() 年使用天然气
年使用天然气![]() 立方米,则小红家
立方米,则小红家![]() 年需缴纳的天然气费为多少元?
年需缴纳的天然气费为多少元?
![]() 依此方案计算,若王先生家
依此方案计算,若王先生家![]() 年实际缴纳天然气费
年实际缴纳天然气费![]() 元,求该户
元,求该户![]() 年使用天然气多少立方米?
年使用天然气多少立方米?
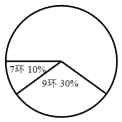
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.