��Ŀ����
����Ŀ����ѧ���⣺����![]() ������m��n��������������m��2��n��1����
������m��n��������������m��2��n��1����
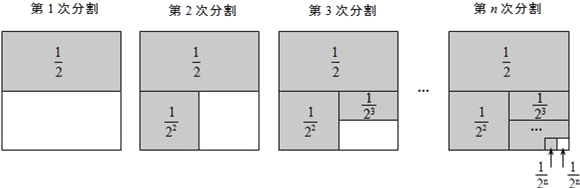
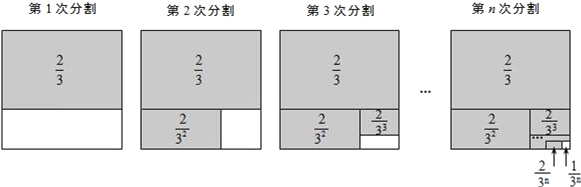
̽�����⣺Ϊ����������ѧ���⣬�����������ν�ϵ�˼�뷽����ͨ�����ϵطָ�һ�����Ϊ1�������Σ���������ϵ�ͼ���ͼ������ؽ������������ȡһ���������⻯�IJ���������̽����
̽��һ������![]() ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ȷ֣�������Ӱ���ֵ����֮��Ϊ![]() �����հײ��ֵ������
�����հײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ�� ![]() =1��
=1��![]() ��
��
̽����������![]() ��
��
��1�ηָ�������ε�������ȷ֣�������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣���Ӱ���ֵ����֮��Ϊ![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ�����������ȷ֣�����
��
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ����������ȷ֣�������Ӱ���ֵ����֮��Ϊ![]() �����հײ��ֵ������
�����հײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ�� ![]() =1��
=1��![]() ��
��
����ͬ����2����![]() =
=![]() .
.
̽����������![]() ��
��
����������������ֻ������n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ�����������д��̽�����̣�

������⣺����![]() ��
��
��ֻ�軭����n�ηָ�ͼ����ͼ�ϱ�ע��Ӱ��������������������գ�
���ݵ�n�ηָ�ͼ�ɵõ�ʽ����������������
���ԣ� ![]() =��������������
=��������������
�ع�Ӧ�ã�����![]() ��
��
���𰸡��𰸼�����.
�����������������̽����������̽�����ķָ�����ν��зָȻ���ʾ����Ӱ���ֵ�������ٳ���3���ɣ�
������⣺����̽�����ķָ�����ηָȻ���ʾ����Ӱ���ֵ���������ٳ��ԣ�m-1�����ɵý⣻
�ع�Ӧ�ã��Ȱ�ÿһ�������ֳ�1��ȥһ��������Ȼ��Ӧ�ù�ʽ���м��㼴�ɵý⣮
���������̽��������1�ηָ�������ε�����ĵȷ֣�
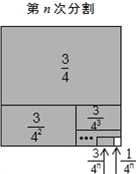
������Ӱ���ֵ����Ϊ![]() ��
��
��2�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�
��Ӱ���ֵ����֮��Ϊ![]() ��
��
��3�ηָ���ϴηָ�ͼ�пհײ��ֵ���������ĵȷ֣�
����
��n�ηָ���ϴηָ�ͼ�пհײ��ֵ��������ĵȷ֣�
������Ӱ���ֵ����֮��Ϊ�� ![]()
���Ŀհײ��ֵ������![]() ��
��
���ݵ�n�ηָ�ͼ�ɵõ�ʽ�� ![]() =1��
=1��![]() ��
��
����ͬ����3����![]() =
=![]() ��
��
������⣺ ![]() ��
��
![]() ��
��
�ʴ�Ϊ�� ![]() =1��
=1��![]() ��
�� ![]() ��
��
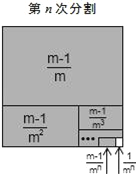
�ع�Ӧ�ã� ![]() ��
��
=1��![]() +1��
+1��![]() +1��
+1��![]() +��+1��
+��+1��![]() ��
��
=n����![]() +
+![]() +
+![]() +��+
+��+![]() ����
����
=n����![]() ��
��![]() ����
����
=n��![]() +
+![]() ��
��