题目内容
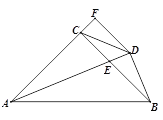
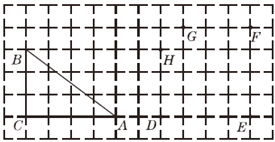
【题目】如图所示，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点分别位于小正方形的顶点上.
（1）现以D，E，F，G，H中的三个点为顶点画三角形，在所画的三角形中与△ABC不全等但面积相等的三角形是 （只需要填一个三角形）；
（2）先从D，E两个点中任意取一个点，再从F，G，H三个点中任意取两个不同的点，以所取的这三个点为顶点画三角形，画树状图求所画三角形与△ABC面积相等的概率.
【答案】（1）△DFG或△DHF；(2)
.
【解析】试题分析：本题综合考查了三角形的面积和概率.（1）、根据“同（等）底同（等）高的三角形面积相等”进行解答；（2）、画树状图求概率.
试题解析：（1）、△DFG或△DHF；
（2）、画树状图如图所示：
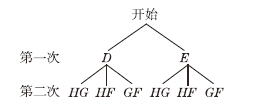
由树状图可知共有6种等可能结果， 其中与△ABC面积相等的有3种，即△DHF，△DGF，△EGF，
所以所画三角形与△ABC面积相等的概率P=
答：所画三角形与△ABC面积相等的概率为
练习册系列答案
相关题目
