题目内容
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1 , △2 , △3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( ) 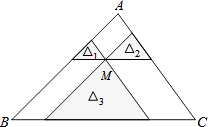
A.49
B.64
C.100
D.81
【答案】D
【解析】解:因为△1、△2、△3的面积比为4:9:16, 所以他们对应边边长的比为2:3:4,
又因为四边形BDMG与四边形CEMH为平行四边形,
所以DM=BG,EM=CH,
设DM为2x,则ME=3x,GH=4x,
所以BC=BG+GH+CH=DM+GH+ME=2x+3x+4x=9x,
所以BC:DM=9x:2x=9:2,
由相似三角形面积比等于相似比的平方,可得出:S△ABC:S△FDM=81:4,
所以△ABC的面积=81.
故选:D.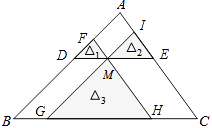
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
【题目】已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | ﹣1 | 0 | m | 8 | … |
(1)可求得m的值为;
(2)求出这个二次函数的解析式;
(3)当y>3时,x的取值范围为 .