题目内容
如图,在Rt△ABC中,∠ACB=900,点D是斜边AB的中点,DE⊥AC,垂足为E,若DE=2,CD=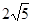 ,则BE的长为
,则BE的长为 
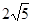 ,则BE的长为
,则BE的长为 
4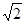
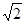
由点D为AB的中点,DE=2,求得BC,在直角三角形CDE中求得CE,在直角三角形CEB中从而求得BE得长.
解:∵在Rt△ABC中,∠ACB=90°,DE⊥AC,
∴DE∥BC,
∵点D为AB的中点,DE=2,
∴BC=4,
∵DE⊥AC,垂足为E,若DE=2,CD=2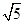 ,
,
在Rt△CDE中,由勾股定理得CE=4,
∵在Rt△BCE中,∠ACB=90°,
BE=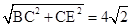 .
.
故答案为:4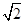 .
.
解:∵在Rt△ABC中,∠ACB=90°,DE⊥AC,
∴DE∥BC,
∵点D为AB的中点,DE=2,
∴BC=4,
∵DE⊥AC,垂足为E,若DE=2,CD=2
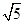 ,
,在Rt△CDE中,由勾股定理得CE=4,
∵在Rt△BCE中,∠ACB=90°,
BE=
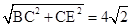 .
.故答案为:4
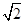 .
.
练习册系列答案
相关题目





 ∥AB,F是
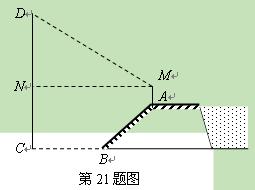
∥AB,F是 的横断面是梯形,背水坡AB的坡比
的横断面是梯形,背水坡AB的坡比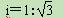 (指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留
(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留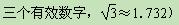
 »1.414,
»1.414, »1.732,
»1.732, »2.449,供选用)
»2.449,供选用)
