题目内容
(2011•广元)如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.
(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证: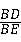 =
=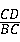 ;
;
(3)若BC=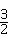 AB,求tan∠CDF的值.
AB,求tan∠CDF的值.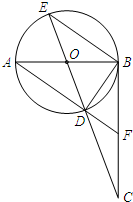
(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:
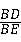 =
=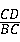 ;
;(3)若BC=
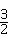 AB,求tan∠CDF的值.
AB,求tan∠CDF的值.
解:(1)∠CBD与∠CEB相等,
证明:∵BC切⊙O于点B,
∴∠CBD=∠BAD,
∵∠BAD=∠CEB,
∴∠CEB=∠CBD,
(2)证明:∵∠C=∠C,∠CEB=∠CBD,
∴∠EBC=∠BDC,
∴△EBC∽△BDC,
∴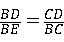 ,
,
(3)∵AB、ED分别是⊙O的直径,
∴AD⊥BD,即∠ADB=90°,
∵BC切⊙O于点B,
∴AB⊥BC,
∵BC=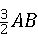 ,
,
∴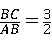 ,
,
设BC=3x,AB=2x,
∴OB=OD=x,
∴OC=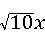 ,
,
∴CD=(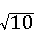 ﹣1)x,
﹣1)x,
∵AO=DO,
∴∠CDF=∠A=∠DBF,
∴△DCF∽△BCD,
∴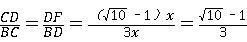 ,
,
∵tan∠DBF=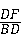 =
=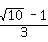 ,
,
∴tan∠CDF=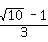 .
.
证明:∵BC切⊙O于点B,
∴∠CBD=∠BAD,
∵∠BAD=∠CEB,
∴∠CEB=∠CBD,
(2)证明:∵∠C=∠C,∠CEB=∠CBD,
∴∠EBC=∠BDC,
∴△EBC∽△BDC,
∴
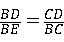 ,
,(3)∵AB、ED分别是⊙O的直径,
∴AD⊥BD,即∠ADB=90°,
∵BC切⊙O于点B,
∴AB⊥BC,
∵BC=
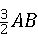 ,
,∴
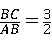 ,
,设BC=3x,AB=2x,
∴OB=OD=x,
∴OC=
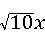 ,
,∴CD=(
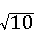 ﹣1)x,
﹣1)x,∵AO=DO,
∴∠CDF=∠A=∠DBF,
∴△DCF∽△BCD,
∴
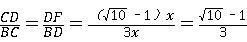 ,
,∵tan∠DBF=
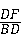 =
=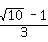 ,
,∴tan∠CDF=
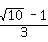 .
.略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, )
)


 .
. ∥AB,F是
∥AB,F是