题目内容
操作探究:图1a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图1b的形状拼成一个正方形.
(1)你认为图1b中的阴影部分的正方形的边长等于多少?______
(2)请用两种不同的方法求图1b中阴影部分的面积.

方法1:______;
方法2:______;
(3)观察图1b你能写出下列三个代数式之间的等量关系吗?代数式:(m+n)2,(m-n)2,mn.______;
(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,求(a-b)2的值.
(5)已知:如图2,现有的a×a,b×b正方形和a×b的矩形纸片若干块,试选用这些纸片(每种至少用一次)在如图3的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,作出的图中必须保留拼图的痕迹),使拼出的矩形面积为2a2+5ab+2b2,并标出此矩形的长和宽.
(1)你认为图1b中的阴影部分的正方形的边长等于多少?______
(2)请用两种不同的方法求图1b中阴影部分的面积.

方法1:______;
方法2:______;
(3)观察图1b你能写出下列三个代数式之间的等量关系吗?代数式:(m+n)2,(m-n)2,mn.______;
(4)根据(3)题中的等量关系,解决如下问题:若a+b=7,ab=5,求(a-b)2的值.
(5)已知:如图2,现有的a×a,b×b正方形和a×b的矩形纸片若干块,试选用这些纸片(每种至少用一次)在如图3的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,作出的图中必须保留拼图的痕迹),使拼出的矩形面积为2a2+5ab+2b2,并标出此矩形的长和宽.
(1)小长方形的长为2m÷2=m,
宽为2n÷2=n,
阴影部分正方形的边长=m-n;
(2)方法1:(m-n)2,
方法2:(m+n)2-4mn;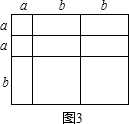
(3)(m-n)2=(m+n)2-4mn;
故答案为:m-n;(m-n)2,(m+n)2-4mn;(m-n)2=(m+n)2-4mn;
(4)∵a+b=7,ab=5,
∴(a-b)2=(a+b)2-4ab=72-4×5=49-20=29;
(5)如图所示,长为a+2b,
宽为:2a+b.
宽为2n÷2=n,
阴影部分正方形的边长=m-n;
(2)方法1:(m-n)2,
方法2:(m+n)2-4mn;

(3)(m-n)2=(m+n)2-4mn;
故答案为:m-n;(m-n)2,(m+n)2-4mn;(m-n)2=(m+n)2-4mn;
(4)∵a+b=7,ab=5,
∴(a-b)2=(a+b)2-4ab=72-4×5=49-20=29;
(5)如图所示,长为a+2b,
宽为:2a+b.

练习册系列答案
相关题目