��Ŀ����
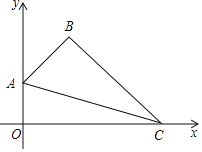
����Ŀ����ͼ![]() ������OABC�Ķ���A��C������ֱ�Ϊ��4��0������0��6����ֱ��AD��BC�ڵ�D��tan��OAD=2��������
������OABC�Ķ���A��C������ֱ�Ϊ��4��0������0��6����ֱ��AD��BC�ڵ�D��tan��OAD=2��������![]() ��A��D���㣮
��A��D���㣮
��![]() �����D�������������M1�ı���ʽ��
�����D�������������M1�ı���ʽ��
��![]() ����P��������M1�Գ�����һ���㣬����CPA=90��ʱ�����������������ĵ�P�����꣮
����P��������M1�Գ�����һ���㣬����CPA=90��ʱ�����������������ĵ�P�����꣮
��![]() ����ͼ
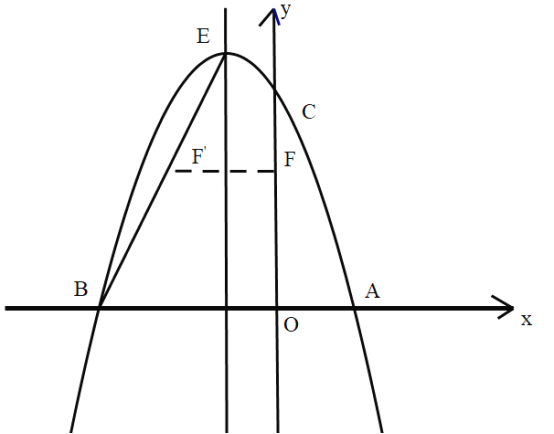
����ͼ![]() ����E��0��4��������AE����������M1��ͼ������ƽ��m(m>0)����λ�õ�������M2��
����E��0��4��������AE����������M1��ͼ������ƽ��m(m>0)����λ�õ�������M2��
�����Dƽ�ƺ�Ķ�Ӧ��Ϊ��D'������D'ǡ������ֱ��AE��ʱ����m��ֵ��
�ڵ�![]() ʱ����������M2��ֱ��AE���������㣬��m��ȡֵ��Χ��
ʱ����������M2��ֱ��AE���������㣬��m��ȡֵ��Χ��
���𰸡���1��D��1��6����������M1�ı���ʽΪy����2x2+8x����2����2��3+![]() ������2��3��
������2��3��![]() ������3����m��3����2+
������3����m��3����2+![]() ��m��
��m��![]()
��������
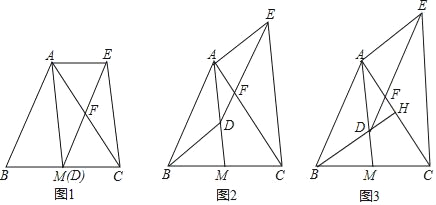
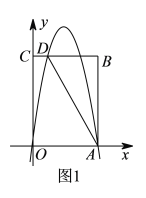
��1����ͼ1�У���DH��OA��H�����ı���CDHO�Ǿ��Σ���Rt��ADH�У���ֱ�������Σ������D���꣬���ô���ϵ�������ɽ�����⣻
��2����ͼ1��1�У���P��2��m�����ɡ�CPA��90�㣬�ɵ�PC2+PA2��AC2���ɵ�22+��m��6��2+22+m2��42+62���ⷽ�̼��ɣ�
��3�������D������ꣻ�����������飬�����б�ʽ����0�������������ֱ��AE����������ʱ��m�ķ�Χ�������x��mʱ�����ƽ�ƺ����������ֱ��AE�Ľ���ĺ����ꣻ��������Ľ��ۼ����жϣ�
�⣺��1����ͼ1�У���DH��OA��H�����ı���CDHO�Ǿ��Σ�
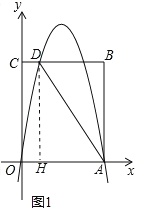
���ı���CDHO�Ǿ��Σ�
��OC��DH��6��
��tan��DAH��![]() ��2��
��2��
��AH��3��
��OA��4��
��CD��OH��1��
��D��1��6����
��D��1��6����A��4��0������y��ax2+bx������![]() ��
��
���![]() ��
��
��������M1�ı���ʽΪy����2x2+8x��
��2����ͼ1��1�У���P��2��m����
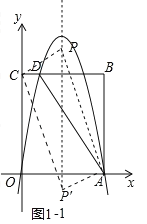
�ߡ�CPA��90�㣬
��PC2+PA2��AC2��
��22+��m��6��2+22+m2��42+62��
���m��3��![]() ��
��
��P��2��3+![]() ����P�䣨2��3��
����P�䣨2��3��![]() ����
����
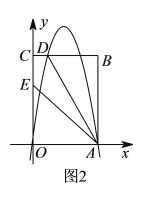
��3������ͼ2�У�

��ֱ֪��AE�Ľ���ʽΪy����x+4��
x��1ʱ��y��3��
��D�䣨1��3����
ƽ�ƺ�������ߵĽ���ʽΪy����2x2+8x��m��
�ѵ�D���������ɵ�3����2+8��m��
��m��3��
����![]() ����ȥy�õ�2x2��9x+4+m��0��
����ȥy�õ�2x2��9x+4+m��0��
����������ֱ��AE����������ʱ������0��
��92��4��2����4+m����0��
��m��![]() ��
��
��x��mʱ����m+4����2m2+8m��m�����m��2+![]() ��2��
��2��![]() ����ȥ����
����ȥ����
������������2+![]() ��m��
��m��![]() ʱ��������M2��ֱ��AE���������㣮
ʱ��������M2��ֱ��AE���������㣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�