题目内容
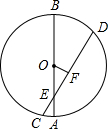 如图,在⊙O中,直径AB与弦CD相交于点E,OF⊥CD,垂足为F.设已知BE=5,AE=
如图,在⊙O中,直径AB与弦CD相交于点E,OF⊥CD,垂足为F.设已知BE=5,AE=| 1 |
| 2 |
考点:垂径定理,勾股定理
专题:
分析:先根据BE=5,AE=
OE得出AE,OE,OA的长,再由垂径定理得出CF=DF,在Rt△ODF中根据勾股定理可得出DF的长,根据CD=2DF即可得出结论.
| 1 |
| 2 |
解答: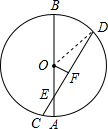 解:连接OD,
解:连接OD,
∵BE=5,AE=
OE,
∴AE=1,OE=2,OA=3,
∴OD=OA=3,
∵OF⊥CD,
∴CF=DF,
在Rt△ODF中,
∵DF=
=2
,
∴CD=2DF=4
.
 解:连接OD,
解:连接OD,∵BE=5,AE=
| 1 |
| 2 |
∴AE=1,OE=2,OA=3,
∴OD=OA=3,
∵OF⊥CD,
∴CF=DF,
在Rt△ODF中,
∵DF=
| OD2-OF2 |
| 2 |
∴CD=2DF=4
| 2 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
写出下列的代数式中,错误的是( )
| A、x,y的平方差是:x2-y2 | ||||
B、甲数是a,甲数是乙数的
| ||||
| C、x的3倍与y的35%的和:3x+35%y | ||||
D、x除以y与3的和的平方:(
|
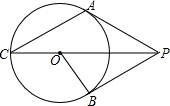 如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为( )
如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为( )| A、4 | ||
B、2
| ||
C、2
| ||
D、3
|
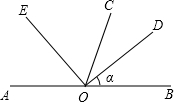 如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α的余角相等的角是
如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α的余角相等的角是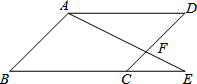 如图,?ABCD中,E为BC延长线上一点,AE交CD于点F,若
如图,?ABCD中,E为BC延长线上一点,AE交CD于点F,若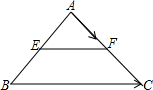 已知:如图,EF是△ABC的中位线,设
已知:如图,EF是△ABC的中位线,设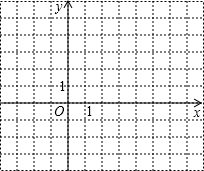 已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).