Question

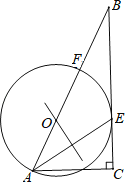
【题目】AD是△ABC的中线，G是AD上任意一点时（点G不与A重合），过点G的直线交边AB于E，交射线AC于点F，设AE＝xAB，AF＝yAC（x、y≠0）．

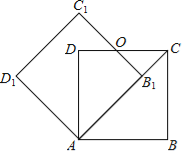
（1）如图1，若点G与D重合，△ABC为等边三角形，且∠BDE＝30°，证明：△AEF∽△DEA；

（2）如图2，若点G与D重合，证明：＝2；

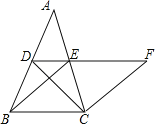
（3）如图3，若AG＝nAD，x＝，y＝，直接写出n的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）n＝

【解析】

（1）先判断出∠BAD＝30°，再判断出∠F＝30°＝∠BAD，即可得出结论；

（2）过C作CH∥AB交EF于H，先判断出△DEB≌△DHC，得出CH＝BE，再判断出△FCH∽△FAE，即可得出结论；

（3）先判断出点E是AB的中点，进而得出DE是△ABC的中位线，得出DE＝AC，DE∥AC，进而得出△DGE∽△AGF，即可得出结论．

解：（1）∵△ABC为等边三角形，

∴∠BAC＝∠B＝60°，AB＝AC，

∵AD是△ABC的中线，

∴∠BAD＝∠BAC＝30°，

∵∠BDE＝30°，

∴EF⊥AB，

∴∠F＝30°＝∠BAD，

∵∠AED＝∠FEA＝90°，

∴△AEF∽△DEA；

（2）如图2，过C作CH//AB交EF于H，

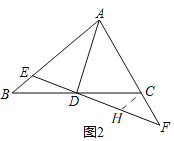
∴∠B＝∠DCH，∠BED＝∠CHD，

∵AD是△ABC的中线，

∴BD＝CD，

∴△DEB≌△DHC（AAS），

∴CH＝BE，

∵CH//AB，

∴△FCH∽△FAE，

∴＝，

∴＝，

∵＝，＝，

∴＝1﹣＝1﹣，＝﹣1＝﹣1

∴1﹣＝﹣1，

∴+ ＝2；

（3）如图3，

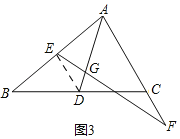
∵y＝，

∴AF＝AC，

∴AC＝AF，

∵x＝，

∴AE＝AB，

∴点E是AB的中点，

∵AD是△ABC的中线，

∴点D是BC的中点，

∴DE＝AC＝AF＝AF，DE∥AC，

∴△DGE∽△AGF，

∴＝，

∴DG＝AG，

∴AD＝AG+DG＝AG+AG＝AG，

∴AG＝AD＝nAD，

∴n＝．