Question

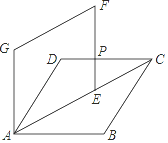
【题目】如图，在菱形ABCD中，AB＝2，∠BAD＝60°，将菱形ABCD绕点A逆时针方向旋转，对应得到菱形AEFG，点E在AC上，EF与CD交于点P，则DP的长是________.

Answer 1

【答案】-1

【解析】

连接AD交AC于O,由菱形的性质得出CD＝AB＝2，∠BCD＝∠BAD＝60°，∠ACD＝∠BAC＝∠BAD＝30°，OA＝OC，AC⊥BD，由直角三角形性质求出OB＝AB＝1，OA＝OB＝，得出AC＝2，由旋转的性质可得AE＝AB＝2，∠EAG＝∠BAD＝60°，得出CE＝AC﹣AE＝2﹣2，证出∠CPE＝90°，由直角三角形的性质得出PE＝CE＝﹣1，PC＝PE＝3﹣，即可得出结果.

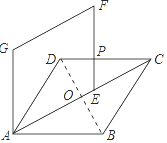
如图所示，连接BD交AC于O，

∵四边形ABCD是菱形，

∴CD＝AB＝2，∠BCD＝∠BAD＝60°，∠ACD＝∠BAC＝∠BAD＝30°，OA＝OC，AC⊥BD，

∴OB＝AB＝1，

∴OA＝OB＝，

∴AC＝2，

由旋转的性质得：AE＝AB＝2，∠EAG＝∠BAD＝60°，

∴CE＝AC﹣AE＝2﹣2，

∵四边形AEFG是菱形，

∴EF∥AG，

∴∠CEP＝∠EAG＝60°，

∴∠CEP+∠ACD＝90°，

∴∠CPE＝90°，

∴PE＝CE＝﹣1，PC＝PE＝3﹣，

∴DP＝CD﹣PC＝2﹣（3﹣）＝﹣1.

故答案为：﹣1.