题目内容
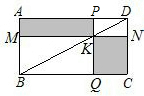
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以2cm/s的速度运动,同时点F从点B出发沿射线BC以3cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF.
(2)①当t为何值时,四边形ACFE是平行四边形;②当t为何值时,以A、F、C、E为顶点的四边形是直角梯形.

(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF.
(2)①当t为何值时,四边形ACFE是平行四边形;②当t为何值时,以A、F、C、E为顶点的四边形是直角梯形.

(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS);
(2)①由题意得:AE=2t,CF=3t-6.
若四边形ACFE是平行四边形,则有CF=AE,则2t=3t-6,
解得t=6.
所以,当t=6时,四边形ACFE是平行四边形;
②情形一:四边形AFCE为直角梯形时,AF⊥BC或CE⊥AG.
当AF⊥BC时,则BF=3t=3,解得t=1;
当CE⊥AG,则AE=2t=3,解得t=1.5,符合题意.
情形二:若四边形ACFE是直角梯形时,此时EF⊥AG.
则BF-AE=3,即3t-2t=3,解得t=3,符合题意;
综上所述,当t=1s或1.5s或3s时,以A、F、C、E为顶点的四边形是直角梯形.
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(AAS);
(2)①由题意得:AE=2t,CF=3t-6.
若四边形ACFE是平行四边形,则有CF=AE,则2t=3t-6,
解得t=6.
所以,当t=6时,四边形ACFE是平行四边形;
②情形一:四边形AFCE为直角梯形时,AF⊥BC或CE⊥AG.
当AF⊥BC时,则BF=3t=3,解得t=1;
当CE⊥AG,则AE=2t=3,解得t=1.5,符合题意.
情形二:若四边形ACFE是直角梯形时,此时EF⊥AG.
则BF-AE=3,即3t-2t=3,解得t=3,符合题意;
综上所述,当t=1s或1.5s或3s时,以A、F、C、E为顶点的四边形是直角梯形.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 内,画出使
内,画出使 的一个点
的一个点 ,并说明理由.
,并说明理由. 的所有的点
的所有的点 .工人师傅想用它裁出两块全等的、面积最大的
.工人师傅想用它裁出两块全等的、面积最大的 和
和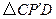 钢板,且
钢板,且 .请你在图③中画出符合要求的点
.请你在图③中画出符合要求的点 ,并求出
,并求出