题目内容
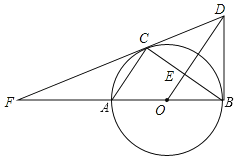
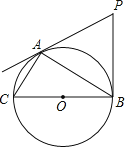
【题目】如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
【答案】(1)证明见解析;(2)![]() cm.
cm.
【解析】
(1)根据PA,PB是切线,∠P=60°,判断出△PAB是正三角形;(2)由等边三角形的性质可得PB=AB=2cm,∠PBA=60°,由圆周角定理和切线的性质可得∠CAB=90°,∠PBC=90°,由锐角三角函数可求AC的长;
解:
(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC=![]() ,
,
∴AC=![]() cm.
cm.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目