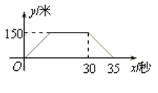
题目内容
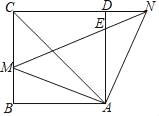
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)根据正方形的性质、全等三角形的判定定理证明△BAM≌△DAN,根据全等三角形的性质证明;
(2)证明△AMC∽△AEN,根据相似三角形的性质证明.
详解:(1)∵四边形ABCD是正方形,∴ AB=AD,∠BAD=90°,
又∵∠MAN=90°,∴∠BAM=∠DAN.
在△BAM和△DAN中,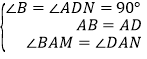 ,
,
∴△BAM≌△DAN,∴AM=AN;
(2)四边形ABCD是正方形,∴∠CAD=45°.
∵∠CAD=2∠NAD,∠BAM=∠DAN,
∴∠MAC=45°,∴∠MAC=∠EAN,
又∠ACM=∠ANE=45°,∴△AMC∽△AEN,
∴![]() =
=![]() ,∴ANAM=ACAE,∴AM2=ACAE.
,∴ANAM=ACAE,∴AM2=ACAE.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目