题目内容
【题目】为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：
港口 | 运费（元/吨） | |
甲库 | 乙库 | |
A港 | 14 | 20 |
B港 | 10 | 8 |
（1）设从甲仓库运送到A港口的物资为x吨，用含x的式子填写下表：
港口 | 运费（元/吨） | |
甲库 | 乙库 | |
A港 | x | |
B港 | ||
（2）求总费用y（元）与x（箱）之间的函数关系式，并写出x的取值范围；
（3）求出最低费用，并说明费用最低时的调配方案．
【答案】
（1）100﹣x；80﹣x；x﹣30
（2）解：y=14x+10（80﹣x）+20（100﹣x）+8（x﹣30）=﹣8x+2560，
由题意得：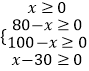 
，
∴不等式的解集为：30≤x≤80，
∴总费用y（元）与x（箱）之间的函数关系式为：y=﹣8x+2560（30≤x≤80）；
（3）解：∵﹣8＜0，
∴y随x的增大而减小，
∴当x=80时，y有最小值，y=﹣8×80+2560=1920，
答：最低费用为1920元，此时的调配方案为：把甲仓库的全部运往A港口，再从乙仓库运20吨到A港口，乙仓库余下的50吨全部分运往B港口．
【解析】解：（1）设从甲仓库运送到A港口的物资为x吨，则甲仓库运送到B港口的物资为（80﹣x）吨，乙仓库运送到A港口的物资为（100﹣x）吨，乙仓库运送到B港口的物资为70﹣（100﹣x）=（x﹣30）吨， 故答案为：100﹣x，80﹣x，x﹣30；
（1）设从甲仓库运送到A港口的物资为x吨，因为甲仓库一共有物资80吨，所以甲仓库运送到B港口的物资为（80﹣x）吨，因为A港口需要运送100吨物资，所以还要从乙仓库运送到A港口的物资为（100﹣x）吨，又因为乙仓库存有70吨物资，所以余下的物资：70﹣（100﹣x）=（x﹣30）吨，都要运到B港口；（2）总费用=物资数量×运费，化成一般式即可，将甲、乙两仓库运往A、B两港口的物资数分别大于等于0，列不等式可求其x的取值范围；（3）根据一次函数的增减性求得最小值，并写出调配方案．
