题目内容
【题目】如图，平行四边形ABCD的对角线AC，BD交于点O，△AOD是正三角形，AD=4，则平行四边形ABCD的面积为 ．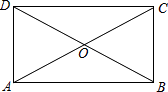 
【答案】16 
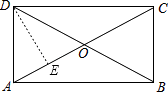
【解析】解：作DE⊥AC于E， ∴∠AED=90°．
∵△AOD是正三角形，
∴AD=DO=AO，AO=EO= 
AO，∠ADO=∠DAO=60°，
∴∠ADE=30°．
∵AD=4，
∴AE=2．
在Rt△ADE中，由勾股定理，得
DE=2 ，
∴S△AOD= ×4×2 =4 ．
∵四边形ABCD是平行四边，
∴S△AOD=S△DOC=S△BOC=S△AOB ，
∴平行四边形ABCD的面积=4×4 =16 ．
所以答案是：16 ．
【考点精析】关于本题考查的等边三角形的性质，需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案．
练习册系列答案
名校课堂系列答案
相关题目
【题目】为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：
港口 | 运费（元/吨） | |
甲库 | 乙库 | |
A港 | 14 | 20 |
B港 | 10 | 8 |
（1）设从甲仓库运送到A港口的物资为x吨，用含x的式子填写下表：
港口 | 运费（元/吨） | |
甲库 | 乙库 | |
A港 | x | |
B港 | ||
（2）求总费用y（元）与x（箱）之间的函数关系式，并写出x的取值范围；
（3）求出最低费用，并说明费用最低时的调配方案．
