题目内容
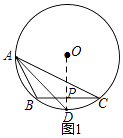
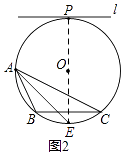
【题目】已知△ABC内接于⊙O,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出∠BAC的平分线(保留作图痕迹,不写作法). 
(1)如图1,P是BC边的中点;
(2)如图2,直线l与⊙O相切于点P,且l∥BC.
【答案】
(1)解:如图所示,AD 即为所求;
(2)解:如图所示,AE即为所求.
【解析】(1)连接OP并延长,交⊙O于D,根据P是BC边的中点,可得OD垂直平分BC,进而得到点D为 ![]() 的中点,连接AD,则∠BAD=∠CAD,因此AD即为所求;(2)连接PO并延长,交⊙O于E,根据直线l与⊙O相切于点P,且l∥BC,可得PE垂直平分BC,进而得到点E为
的中点,连接AD,则∠BAD=∠CAD,因此AD即为所求;(2)连接PO并延长,交⊙O于E,根据直线l与⊙O相切于点P,且l∥BC,可得PE垂直平分BC,进而得到点E为 ![]() 的中点,连接AE,则∠BAE=∠CAE,因此AE即为所求.
的中点,连接AE,则∠BAE=∠CAE,因此AE即为所求.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目