题目内容
【题目】如图，已知抛物线y=﹣x2+2x+3与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，连接BC．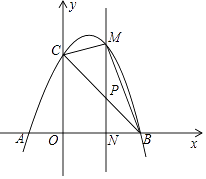
（1）求A，B，C三点的坐标；
（2）若点P为线段BC上一点（不与B，C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求点P的坐标；
（3）在（2）的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在一点Q，使得△CNQ为直角三角形，求点Q的坐标．
【答案】
（1）
解：在y=﹣x2+2x+3中，令x=0可得y=3，
∴C（0，3），
令y=0，可得﹣x2+2x+3=0，解得x=3或x=﹣1，
∴A（﹣1，0），B（3，0）
（2）
解：设直线BC的解析式为y=kx+b，则有 
，解得 
，
∴直线BC的解析式为y=﹣x+3．
设P（t，﹣t+3），则M（t，﹣t2+2t+3），
∴PM=（﹣t2+2t+3）﹣（﹣t+3）=﹣t2+3t．
∴S△BCM= 
PM（ON+BN）= PMOB= ×3（﹣t2+3t）=﹣ 
（t﹣ ）2+ 
，
∵﹣ ＜0，
∴当t= 时，△BCM的面积最大，此时P点坐标为（ ， ）
（3）
解：∵y=﹣x2+2x+3=﹣（x﹣1）2+4，
∴抛物线的对称轴为直线x=1，
∴设Q（1，m），且C（0，3），N（ ，0），
∴CN= 
= 
，CQ= 
= 
，NQ= 
= 
，
∵△CNQ为直角三角形，
∴分点C为直角顶点、点Q为直角顶点和点N为直角顶点三种情况：
①当点C为直角顶点时，则有CN2+CQ2=NQ2，
即（ ）2+（m2﹣6m+10）= 
+m2，解得m= 
，
此时Q点坐标为（1， ）；
②当点Q为直角顶点时，则有NQ2+CQ2=CN2，
即（m2﹣6m+10）+ +m2=（ ）2，解得x= 
或x= 
，
此时Q点坐标为（1， ）或（1， ）；
③当点N为直角顶点时，则有NQ2+CN2=CQ2，
即（ ）2+ +m2=m2﹣6m+10，解得m=﹣ ，
此时Q点坐标为（1，﹣ ）；
综上可知Q点的坐标为（1， ）或（1， ）或（1， ）或（1，﹣ ）
【解析】（1）在抛物线解析式中，令x=0可求得C点坐标，令y=0则可求得A、B的坐标；（2）由B、C的坐标可求得直线BC的解析式为y=﹣x+3，可设P点坐标为（t，﹣t+3），则可表示出M点坐标，则可求得PM的长，从而可用t表示出△BCM的面积，再利用二次函数的性质可求得当△BCM的面积最大时t的值，可求得P点坐标；（3）由（2）可知N点坐标，设Q点坐标为（1，m），则可用m分别表示出QN、QC及CN，分点C为直角顶点、点Q为直角顶点和点N为直角顶点三种情况，分别根据勾股定理可得到关于m的方程，可求得m的值，可求得Q点坐标．
