题目内容
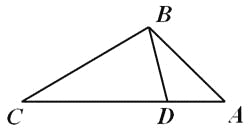
【题目】如图,在△ABC中,AD、BE是中线,它们相交于点F,EG∥BC,交AD于点G.
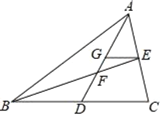
(1)求证:△FGE∽△FDB;
(2)求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由GE∥BC,可得出∠GEF=∠DBF,再结合对顶角相等即可得出△FGE∽△FDB;
(2)根据三角形中线定理以及中位线的定义得出GE=![]() BD、AG=DG,再利用相似三角形的性质得出DF=
BD、AG=DG,再利用相似三角形的性质得出DF=![]() DG,进而即可得出
DG,进而即可得出![]() =
=![]() .
.
解:(1)证明:∵GE∥BC,
∴∠GEF=∠DBF.
又∵∠GFE=∠DFB,
∴△FGE∽△FDB;
(2)如图:
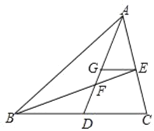
∵AD、BE是中线,EG∥BC,
∴GE为△ADC的中位线,BD=DC,
∴GE=![]() DC=
DC=![]() BD,AG=DG.
BD,AG=DG.
∵△FGE∽△FDB,
∴![]() ,
,
∴DF=![]() DG,
DG,
∴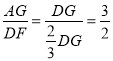 ;
;

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目