��Ŀ����
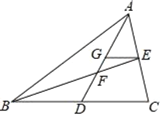
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() .
.
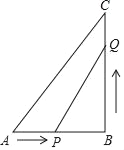
��1����![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() ����
����![]() ��
��![]() ���ٶ��ƶ�����
���ٶ��ƶ�����![]() ��
��![]() �㿪ʼ��
�㿪ʼ��![]() �����
�����![]() ��
��![]() ���ٶ��ƶ�.�����
���ٶ��ƶ�.�����![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ͬʱ�������������룬
ͬʱ�������������룬![]() ���������
���������![]() ��
��
��2����![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �����
�����![]() ��
��![]() ���ٶ��ƶ�����
���ٶ��ƶ�����![]() ��
��![]() �㿪ʼ��
�㿪ʼ��![]() �����
�����![]() ��
��![]() ���ٶ��ƶ�.�����
���ٶ��ƶ�.�����![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ͬʱ�������߶�
ͬʱ�������߶�![]() �ܷ�
�ܷ�![]() �ֳ������ȵ������֣����ܣ�����˶�ʱ�䣻�����ܣ���˵������.
�ֳ������ȵ������֣����ܣ�����˶�ʱ�䣻�����ܣ���˵������.
��3������![]() ���߶�
���߶�![]() �����
�����![]() �������
�������![]() ���ٶ����
���ٶ����![]() �ƶ�����
�ƶ�����![]() ������
������![]() �����
�����![]() �������
�������![]() ���ٶ��ƶ���
���ٶ��ƶ���![]() ��
��![]() ͬʱ�������ʼ����
ͬʱ�������ʼ����![]() �����Ϊ
�����Ϊ![]() ��
��
���𰸡���1��2���4�� ��2���𰸼����� ��3��![]() ���5��
���5��
��������
��1������ֱ�������ε������ʽ��·��=�ٶȡ�ʱ�������⼴�ɣ�
��2���辭��![]() �룬�߶�
�룬�߶�![]() �ܷ�
�ܷ�![]() �ֳ������ȵ������֣��������֮��ĵ�����ϵ���б�ʽ������⣻
�ֳ������ȵ������֣��������֮��ĵ�����ϵ���б�ʽ������⣻
��3��������������ٵ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
�ڵ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ���ӳ�����ʱ���������ۼ������.
���ӳ�����ʱ���������ۼ������.
�⣺��1���辭��![]() �룬
�룬![]() ���������
���������![]() ����������
����������
![]() ��
��
���![]() ��
��![]() ��
��
�����飬![]() ��
��![]() ����������.
����������.
�𣺾���2���4�룬![]() ���������
���������![]() .
.
��2���辭��![]() �룬�߶�
�룬�߶�![]() ��
��![]() �ֳ������ȵ������֣���������
�ֳ������ȵ������֣���������
![]() ��
��
����ɵ�![]() .
.
��![]() .��˷�����ʵ����.
.��˷�����ʵ����.
���߶�![]() ���ܽ�
���ܽ�![]() �ֳ������ȵ�������.
�ֳ������ȵ�������.
��3������![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
�辭��![]() �룬
�룬![]() �����Ϊ
�����Ϊ![]() .
.
��������![]() ��
��![]()
���![]() ����ȥ����
����ȥ����![]() ��
��
��![]() ��
��
����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ���ӳ�����ʱ��
���ӳ�����ʱ��
�辭��![]() �룬
�룬![]() �����Ϊ
�����Ϊ![]() .
.
��������![]() ��
��![]() ��
��
���![]() .
.
�����飬![]() ��������.
��������.
��������������![]() ���5�룬
���5�룬![]() �����Ϊ
�����Ϊ![]() .
.

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�