��Ŀ����
 �Ӽס���������ѡ��һ�⣬������ⶼ����ֻ�Լ���Ʒ֣�
�Ӽס���������ѡ��һ�⣬������ⶼ����ֻ�Լ���Ʒ֣����⣺������x��һԪ���η���x2-2��2-k��x+k2+12=0��ʵ���������£�
��1����ʵ��k��ȡֵ��Χ��
��2����t=
| ��+�� | k |
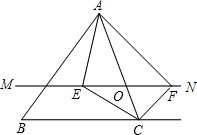
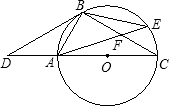
���⣺��ͼ���ڡ�ABC�У���O��AC���ϵ�һ�����㣬����O��ֱ��MN��BC����MN����BCA�Ľ�ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���֤����Ľ��ۣ�
���������⣨1������һԪ���η��̵ĸ����б�ʽ������ɣ�
��2�����ݸ���ϵ���Ĺ�ϵ��k�ķ�Χ������ɣ�
���⣬��֤OE=OC=OF���ó�ƽ���ı���AECF��֤��ECF=90�㣬���ݾ��ε��ж��Ƴ����ɣ�
��2�����ݸ���ϵ���Ĺ�ϵ��k�ķ�Χ������ɣ�
���⣬��֤OE=OC=OF���ó�ƽ���ı���AECF��֤��ECF=90�㣬���ݾ��ε��ж��Ƴ����ɣ�
������⣺�⣺��1����һԪ���η���x2-2��2-k��x+k2+12=0��ʵ����������
�����0����4��2-k��2-4��k2+12����0��
���k��-2��
��2���ɸ���ϵ���Ĺ�ϵ�ã���+��=-[-2��2-k��]=4-2k��
t=
=
=
-2��
��k��-2��
��-4��t��0��
��t����СֵΪ-4��
���⣺����O�˶���AC���е�ʱ���ı���AECF�Ǿ��Σ�
֤����
��MN��BC��
���2=��3��
��CFƽ�֡�ACQ��
���1=��2��
���1=��3��
��OC=OF��
ͬ��OE=OC��
��OE=OF��
��AO=OC��
���ı���AECF��ƽ���ı��Σ�
��CEƽ�֡�BCA����1=��2=
��ACQ��
���BCE=��ECA=
��BCA��
���ECF=
����BCA+��ACQ��=90�㣬
��ƽ���ı���AECF�Ǿ��Σ�
�����0����4��2-k��2-4��k2+12����0��
���k��-2��
��2���ɸ���ϵ���Ĺ�ϵ�ã���+��=-[-2��2-k��]=4-2k��
t=
| ��+�� |
| k |
| 4-2k |
| k |
| 4 |
| k |
��k��-2��
��-4��t��0��
��t����СֵΪ-4��
���⣺����O�˶���AC���е�ʱ���ı���AECF�Ǿ��Σ�
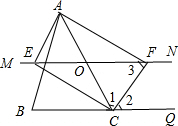
֤����

��MN��BC��
���2=��3��
��CFƽ�֡�ACQ��
���1=��2��
���1=��3��
��OC=OF��
ͬ��OE=OC��
��OE=OF��
��AO=OC��
���ı���AECF��ƽ���ı��Σ�
��CEƽ�֡�BCA����1=��2=
| 1 |
| 2 |
���BCE=��ECA=
| 1 |
| 2 |
���ECF=
| 1 |
| 2 |
��ƽ���ı���AECF�Ǿ��Σ�
���������⿼����ƽ�������ʣ������б�ʽ������ϵ���Ĺ�ϵ��ƽ���ı��ε��ж��;��ε��ж�����Ҫ����ѧ�����ö������������ͼ����������

��ϰ��ϵ�д�
 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
�����Ŀ
 �Ӽס���������ѡ��һ�⼴�ɣ�������ⶼ����ֻ�Լ���Ʒ֣�
�Ӽס���������ѡ��һ�⼴�ɣ�������ⶼ����ֻ�Լ���Ʒ֣� �����ɣ�
�����ɣ� �ڵ�Q��
�ڵ�Q��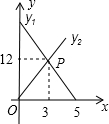 ���߶�y1��y2�ֱ��ʾС����С����B�صľ��루ǧ�ף�������ʱ�䣨Сʱ���Ĺ�ϵ��
���߶�y1��y2�ֱ��ʾС����С����B�صľ��루ǧ�ף�������ʱ�䣨Сʱ���Ĺ�ϵ��
 ����Ϊѡ���⣬�Ӽס���������ѡ��һ�⼴�ɣ�������ⶼ����ֻ�Լ���Ʒ֣�
����Ϊѡ���⣬�Ӽס���������ѡ��һ�⼴�ɣ�������ⶼ����ֻ�Լ���Ʒ֣� ��2013•��üɽ�ж�ģ��ѡ���⣺�Ӽס���������ѡ��һ�⣬������ⶼ����ֻ�Լ���Ʒ֣�
��2013•��üɽ�ж�ģ��ѡ���⣺�Ӽס���������ѡ��һ�⣬������ⶼ����ֻ�Լ���Ʒ֣�