题目内容
从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.甲:小东从A地出发以某一速度向B地走去,同时小明从B地出发以另-速度向A地而行.如图所示,图中
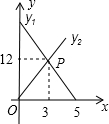 的线段y1、y2分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系.
的线段y1、y2分别表示小东、小明离B地的距离(千米)与所用时间(小时)的关系.(1)试用文字说明:交点P所表示的实际意义;
(2)试求y1、y2的解析式;
(3)试求出A、B两地之间的距离.
乙:如图,?ABCD中,E是BA的延长线上一点,CE与AD交于点F.
(1)求证:△AEF∽△DCF;
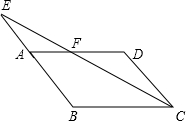
(2)若AB=2AE,△AEF的面积为2
| 2 |
我选做的是
分析:甲题:(1)根据题意表示出交点P所表示的实际意义;
(2)用待定系数法求得函数解析式;
(3)用函数解析式的几何意义可求得两地的距离;
乙题:(1)要根据平行的性质得到相等的角,从而证明△AEF∽△DCF;
(2)用三角形的面积比等于相似比的平方可依次求得△CDF,梯形BCFA的面积,求和即为?ABCD的面积.
(2)用待定系数法求得函数解析式;
(3)用函数解析式的几何意义可求得两地的距离;
乙题:(1)要根据平行的性质得到相等的角,从而证明△AEF∽△DCF;
(2)用三角形的面积比等于相似比的平方可依次求得△CDF,梯形BCFA的面积,求和即为?ABCD的面积.
解答:解:甲:(1)P点表示两人出发3小时后相遇;
(2)设y1=kx+b,y2=tx;把点(3,12),(5,0)代入y1得到k=-6,b=30.
把点(3,12)代入y2得到t=4,所以
y1=-6x+30,y2=4x;
(3)由(2)知,y1=-6x+30,则当x=0时,y1=30,所以AB两地间的距离为30千米.
乙:(1)证明:∵AE∥DC
∴∠E=∠DCF,∠D=∠FAE
∴△AEF∽△DCF.
(2)解:S△DCF=8
,
S△EBC=18
,
SABCD=24
.
(2)设y1=kx+b,y2=tx;把点(3,12),(5,0)代入y1得到k=-6,b=30.
把点(3,12)代入y2得到t=4,所以
y1=-6x+30,y2=4x;
(3)由(2)知,y1=-6x+30,则当x=0时,y1=30,所以AB两地间的距离为30千米.
乙:(1)证明:∵AE∥DC
∴∠E=∠DCF,∠D=∠FAE
∴△AEF∽△DCF.
(2)解:S△DCF=8
| 2 |
S△EBC=18
| 2 |
SABCD=24
| 2 |
点评:主要考查平行四边形的性质和相似三角形的判定以及利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意,根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.

练习册系列答案
相关题目
 从甲、乙两题中选做一题即可.如果两题都做,只以甲题计分.
从甲、乙两题中选做一题即可.如果两题都做,只以甲题计分.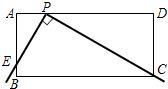 明理由.
明理由.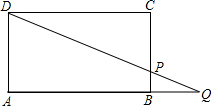 于点Q.
于点Q.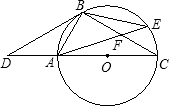 本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
本题为选做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分. (2013•峨眉山市二模)选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
(2013•峨眉山市二模)选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分.