题目内容
从甲、乙两题中选做一题．如果两题都做，只以甲题计分．题甲：若关于x一元二次方程x2-2（2-k）x+k2+12=0有实数根a，β．
（1）求实数k的取值范围；
（2）设t=
| a+β |
| k |
题乙：如图所示，在矩形ABCD中，P是BC边上一点，连接DP并延长，交AB的延长线
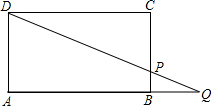于点Q．（1）若
| BP |
| PC |
| 1 |
| 3 |
| AB |
| AQ |
（2）若点P为BC边上的任意一点，求证：
| BC |
| BP |
| AB |
| BQ |
我选做的是
分析：对甲：（1）由于一元二次方程存在两实根，令△≥0求得k的取值范围；
（2）将α+β换为k的表达式，根据k的取值范围得出t的取值范围，求得最小值．
（2）将α+β换为k的表达式，根据k的取值范围得出t的取值范围，求得最小值．
解答：题甲
解：（1）∵一元二次方程x2-2（2-k）x+k2+12=0有实数根a，β，
∴△≥0，
即4（2-k）2-4（k2+12）≥0，
得k≤-2．
（2）由根与系数的关系得：a+β=-[-2（2-k）]=4-2k，
∴t=
=
=
-2，
∵k≤-2，
∴-2≤
-2＜0，
∴-4≤
-2＜-2，
即t的最小值为-4．
题乙：
（1）解：∵AB∥CD，∴
=
=
，即CD=3BQ，
∴
=
=
=
；
（2）证明：四边形ABCD是矩形
∵AB=CD，AB∥DC
∴△DPC∽△QPB
∴
=
-
=
-
=1+
-
=1
∴
-
=1．
解：（1）∵一元二次方程x2-2（2-k）x+k2+12=0有实数根a，β，
∴△≥0，
即4（2-k）2-4（k2+12）≥0，
得k≤-2．
（2）由根与系数的关系得：a+β=-[-2（2-k）]=4-2k，
∴t=
| a+β |
| k |
| 4-2k |
| k |
| 4 |
| k |
∵k≤-2，
∴-2≤
| 4 |
| k |
∴-4≤
| 4 |
| k |
即t的最小值为-4．
题乙：
（1）解：∵AB∥CD，∴
| BP |
| PC |
| BQ |
| CD |
| 1 |
| 3 |
∴
| AB |
| AQ |
| CD |
| CD+BQ |
| 3BQ |
| 3BQ+BQ |
| 3 |
| 4 |
（2）证明：四边形ABCD是矩形
∵AB=CD，AB∥DC
∴△DPC∽△QPB
∴
| DC |
| BQ |
| PC |
| BP |
| BC |
| BP |
| AB |
| BQ |
| BP+PC |
| BP |
| AB |
| BQ |
| PC |
| BP |
| DC |
| BQ |
∴
| BC |
| BP |
| AB |
| BQ |
点评：本题考查了一元二次方程根的判定，另要掌握两根之和、两根之积与系数的关系．
练习册系列答案
名校课堂系列答案
相关题目
从甲、乙两题中选做一题即可．如果两题都做，只以甲题计分．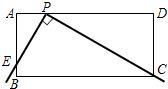
明理由．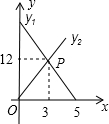
的线段y1、y2分别表示小东、小明离B地的距离（千米）与所用时间（小时）的关系．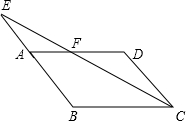
本题为选做题，从甲、乙两题中选做一题即可，如果两题都做，只以甲题计分．
（2013•峨眉山市二模）选做题：从甲、乙两题中选做一题，如果两题都做，只以甲题计分．