��Ŀ����
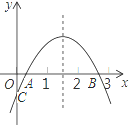
����Ŀ����ͼ�����κ���y=ax2+bx+c��a![]() 0����ͼ����㣨-2,0�����Գ���Ϊֱ��x=1.�����½��ۣ���abc>0����8a+c>0������A��x1��m����B��x2��m�����������ϵ����㣬��x=x1+x2ʱ��y=c����������a��x+2����4-x��=-2������Ϊx1��x2����x1<x2����-2
0����ͼ����㣨-2,0�����Գ���Ϊֱ��x=1.�����½��ۣ���abc>0����8a+c>0������A��x1��m����B��x2��m�����������ϵ����㣬��x=x1+x2ʱ��y=c����������a��x+2����4-x��=-2������Ϊx1��x2����x1<x2����-2![]() x1<x2<4.
x1<x2<4.
���н�����ȷ���У� ��
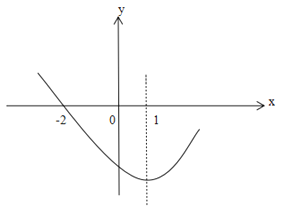
A. 1��B. 2��C. 3��D. 4��
���𰸡�B
��������
���ݶ��κ�����ͼ�������ʼ�������𰸣�
![]() �����߿������ϣ�
�����߿������ϣ�![]() a>0.
a>0.
![]() �����ߵĶԳ�����y���Ҳ࣬
�����ߵĶԳ�����y���Ҳ࣬![]() a��b��ţ�
a��b��ţ�![]() b<0.
b<0.
![]() �����߽�y���ڸ����ᣬ
�����߽�y���ڸ����ᣬ![]() c<0��
c<0��![]() abc>0��
abc>0��![]() ����ȷ.
����ȷ.
![]() �����ߵĶԳ���Ϊx=1��
�����ߵĶԳ���Ϊx=1��![]()
![]() =1��
=1��![]() b=-2a.
b=-2a.
��x=-2ʱ��4a-2b+c=0��![]() 4a+4a+c=0����8a+c=0��
4a+4a+c=0����8a+c=0��![]() �ڴ���.
�ڴ���.
![]() A��x1��m����B��x2��m�����������ϵ����㣬���������ߵĶԳ��ԣ�
A��x1��m����B��x2��m�����������ϵ����㣬���������ߵĶԳ��ԣ�![]() x1+x2=1��2=2��
x1+x2=1��2=2��
![]() ��x=x1+x2ʱ����x=2ʱ��y=4a+2b+c=4a-4a+c=c��
��x=x1+x2ʱ����x=2ʱ��y=4a+2b+c=4a-4a+c=c��![]() ����ȷ.
����ȷ.
![]() �����ߵĶԳ���Ϊx=1������x���һ������Ϊ��-2��0����
�����ߵĶԳ���Ϊx=1������x���һ������Ϊ��-2��0����
![]() ��x�����һ������Ϊ��4��0����
��x�����һ������Ϊ��4��0����![]() ԭ����Ϊ��y=a��x+2����x-4��.
ԭ����Ϊ��y=a��x+2����x-4��.
������a��x+2����4-x��=-2��������a��x+2����x-4��=2������Ϊx1��x2����x1��x2Ϊ��������ֱ��y=2����������ĺ�����.
��![]() x1<x2����x1<-2<4<x2��
x1<x2����x1<-2<4<x2��![]() �ܴ���.
�ܴ���.
������������ȷ�Ľ�����2��.
��ѡB.