题目内容
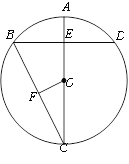
【题目】如图,等边△ABC内接于⊙O,P是弧AB上任一点(点P不与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
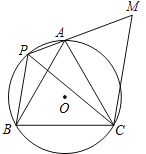
(1)求∠APC的度数.
(2)求证:△PCM为等边三角形.
(3)若PA=1,PB=3,求△PCM的面积.
【答案】(1)∠APC=60°;(2)见解析;(3)S△PCM=4![]() .
.
【解析】
(1)利用同弧所对的圆周角相等即可求得题目中的未知角;
(2)利用同弧所对的圆周角相等即可求得题目中的未知角,进而判定△PCM为等边三角形;
(2)利用上题中得到的相等的角和等边三角形中相等的线段证得两三角形全等,进而利用△PCM为等边三角形,进而求得PH的长,利用三角形的面积公式计算即可.
(1)∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠APC=∠ABC=60°;
(2)∵∠BPC=∠BAC=60°,
∵CM∥BP,
∴∠PCM=∠BPC=60°,
又由(1)得∠APC=60°,
∴△PCM为等边三角形;
(3)解:∵△ABC是等边三角形,△PCM为等边三角形,
∴∠PCA+∠ACM=∠BCP+∠PCA,
∴∠BCP=∠ACM,
在△BCP和△ACM中,
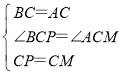 ,
,
∴△BCP≌△ACM(SAS),
∴CM=CP,AM=BP=3,
∴CM=PM=1+3=4,
作PH⊥CM于H,
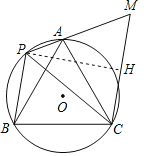
在Rt△PMH中,∠PMH=60°,PM=4,
∴PH=2![]() ,
,
∴S△PCM=![]() PHCM=
PHCM=![]() ×4×2
×4×2![]() =4
=4![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目