题目内容
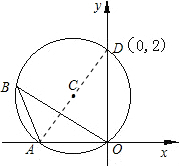
如图,⊙C通过原点,并与坐标轴分别交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A(______);C(______).


连AD,如图,
∵∠AOD=90°,
∴AD为直径,即AD过点C,
又有∠ADO=∠OBA=30°,设OA=x,则AD=2x,
所以(2x)2-x2=22,解得x=
,即OA=
.
∴A点坐标为(-
,0),
又∵C点为AD的中点,
∴C点坐标为(-
,1).
故答案为(-
,0),(-
,1).
∵∠AOD=90°,
∴AD为直径,即AD过点C,
又有∠ADO=∠OBA=30°,设OA=x,则AD=2x,
所以(2x)2-x2=22,解得x=
2
| ||
| 3 |
2
| ||
| 3 |
∴A点坐标为(-
2
| ||
| 3 |
又∵C点为AD的中点,
∴C点坐标为(-
| ||
| 3 |
故答案为(-
2
| ||
| 3 |
| ||
| 3 |


练习册系列答案
相关题目









