题目内容
24、已知正方形ABCD.如图1,E是AD上一点,过A作BE的垂线,交BE于点O,交CD于点H,通过证明△ABE≌△ADH,可得:BE=AH;
(1)如图2,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H,猜想BE与GH的数量关系为
(2)如图3,过正方形ABCD内任意一点作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,猜想EF与GH的数量关系为
(3)当点O在正方形ABCD的边上或外部时,过点O作两条互相垂直的直线,被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗?其中一种情形如图4所示,过正方形ABCD外一点O作互相垂直的两条直线m、n,m与AD、BC的延长线分别交于点E、F,n与AB、DC的延长线分别交于点G、H,试就该图形对你的结论加以证明.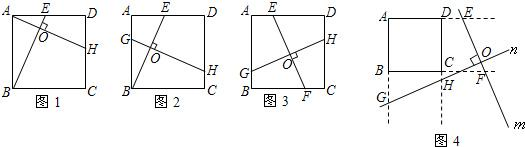
(1)如图2,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H,猜想BE与GH的数量关系为
BE=GH
;(2)如图3,过正方形ABCD内任意一点作两条互相垂直的直线,分别交AD、BC于点E、F,交AB、CD于点G、H,猜想EF与GH的数量关系为
EF=GH
;(3)当点O在正方形ABCD的边上或外部时,过点O作两条互相垂直的直线,被正方形相对的两边(或它们的延长线)截得的两条线段还相等吗?其中一种情形如图4所示,过正方形ABCD外一点O作互相垂直的两条直线m、n,m与AD、BC的延长线分别交于点E、F,n与AB、DC的延长线分别交于点G、H,试就该图形对你的结论加以证明.

分析:(1)(2)根据图形,即可通过观察,测量并且证明得到:BE=GH;
(2)图3中,作EM⊥BC于M,GN⊥CD于N,根据正方形的性质,可以证得:△EMF≌△GNH,即可证得:GH=EF,在图4中同理可以证得.
(2)图3中,作EM⊥BC于M,GN⊥CD于N,根据正方形的性质,可以证得:△EMF≌△GNH,即可证得:GH=EF,在图4中同理可以证得.
解答: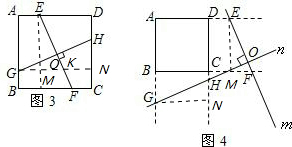 解:(1)BE=GH;
解:(1)BE=GH;
(2)EF=GH;
(3)BE=GH.
证明:图3中,作EM⊥BC,GN⊥CD分别于M,N.
则EM=AB,GN=BC,
∴EM=GN,
∵∠FEM+∠GKE=∠GKE+∠NGH=90°,
∴∠FEM=∠NGH,
又∵∠GNH=∠EMF=90°,
∴△EMF≌△GNH,
∴GH=EF;
在图4中,
∵BC=GN,EM=DC,
又∵BC=DC,
∴GN=EM.
∵在直角△GMB和直角△OMF中,∠GBC=∠COF=90°,∠BCG=∠OCF,
∴∠BGC=∠CFO,
又∵AB∥DC,
∴∠BGC=∠GHN,
∴∠GHN=∠CFE,
又∵在直角△GHN和直角△EFM中,GN=EM,
∴△GHN≌△EFM,
∴GH=EF.
 解:(1)BE=GH;
解:(1)BE=GH;(2)EF=GH;
(3)BE=GH.
证明:图3中,作EM⊥BC,GN⊥CD分别于M,N.
则EM=AB,GN=BC,
∴EM=GN,
∵∠FEM+∠GKE=∠GKE+∠NGH=90°,
∴∠FEM=∠NGH,
又∵∠GNH=∠EMF=90°,
∴△EMF≌△GNH,
∴GH=EF;
在图4中,
∵BC=GN,EM=DC,
又∵BC=DC,
∴GN=EM.
∵在直角△GMB和直角△OMF中,∠GBC=∠COF=90°,∠BCG=∠OCF,
∴∠BGC=∠CFO,
又∵AB∥DC,
∴∠BGC=∠GHN,
∴∠GHN=∠CFE,
又∵在直角△GHN和直角△EFM中,GN=EM,
∴△GHN≌△EFM,
∴GH=EF.
点评:本题主要考查了正方形的性质,把证明线段相等的问题转化为证明三角形全等的问题,正确构造三角形是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
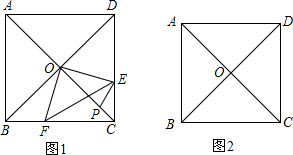
 直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.
直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2. 已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.
已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.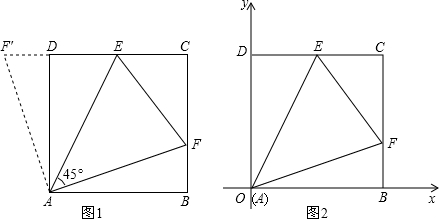
 如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.
如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.