题目内容
(2012•惠山区一模)阅读与证明:
如图,已知正方形ABCD中,E、F分别是CD、BC上的点,且∠EAF=45°,
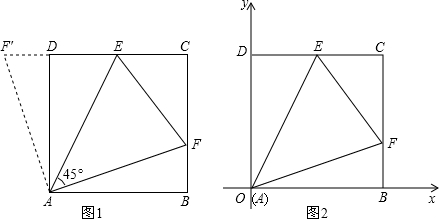
求证:BF+DE=EF.
分析:证明一条线段等于另两条线段的和,常用“截长法”或“补短法”,将线段BF、DE放在同一直线上,构造出一条与BF+DE相等的线段.如图1延长ED至点F′,使DF′=BF,连接A F′,易证△ABF≌△ADF′,进一步证明△AEF≌△AEF′,即可得结论.
(1)请你将下面的证明过程补充完整.
证明:延长ED至F′,使DF′=BF,
∵四边形ABCD是正方形
∴AB=AD,∠ABF=∠ADF′=90°,
∴△ABF≌△ADF’(SAS)
应用与拓展:如图建立平面直角坐标系,使顶点A与坐标原点O重合,边OB、OD分别在x轴、y轴的正半轴上.
(2)设正方形边长OB为30,当E为CD中点时,试问F为BC的几等分点?并求此时F点的坐标;
(3)设正方形边长OB为30,当EF最短时,直接写出直线EF的解析式:
如图,已知正方形ABCD中,E、F分别是CD、BC上的点,且∠EAF=45°,

求证:BF+DE=EF.
分析:证明一条线段等于另两条线段的和,常用“截长法”或“补短法”,将线段BF、DE放在同一直线上,构造出一条与BF+DE相等的线段.如图1延长ED至点F′,使DF′=BF,连接A F′,易证△ABF≌△ADF′,进一步证明△AEF≌△AEF′,即可得结论.
(1)请你将下面的证明过程补充完整.
证明:延长ED至F′,使DF′=BF,
∵四边形ABCD是正方形
∴AB=AD,∠ABF=∠ADF′=90°,
∴△ABF≌△ADF’(SAS)
应用与拓展:如图建立平面直角坐标系,使顶点A与坐标原点O重合,边OB、OD分别在x轴、y轴的正半轴上.
(2)设正方形边长OB为30,当E为CD中点时,试问F为BC的几等分点?并求此时F点的坐标;
(3)设正方形边长OB为30,当EF最短时,直接写出直线EF的解析式:
y=-x+30
| 2 |
y=-x+30
.| 2 |
分析:(1)延长EDF′,使DF′=BF,由ABCD为正方形,根据正方形的四条边相等得到AB=AD,∠ABF=∠ADF′=90°,利用SAS可得出三角形ABF与三角形ADF′全等,根据全等三角形的性质得到AF=AF′,∠BAF=∠DAF′,由∠EAF为45°,得到∠DAE+∠FAB=45°,等量代换可得出∠EAF′=45°,然后利用SAS得到三角形AEF与三角形AEF′,利用全等三角形的对应边相等得到EF=EF′,而EF′=ED+DF′,再将DF′换为BF即可得证;
(2)设BF=a,由CB-FB表示出CF,由EF=ED+FB表示出EF,在直角三角形CEF中,利用勾股定理列出关于a的方程,求出方程的解得到a的值为10,可得出F为BC的三等分点;
(3)当CE=CF时,EF最短,此时△CEF为等腰直角三角形,由题意设出F(30,b),即FB=b,由CB-FB表示出CF,即为CE,由EF=BF+DE=2BF=2b,在直角三角形CEF中,由表示出的CF与CE利用勾股定理表示出EF,可列出关于b的方程,求出方程的解得到b的值,确定出E与F的坐标,设直线EF的解析式为y=kx+b,将E和F的坐标代入得到关于k与b的二元一次方程组,求出方程组的解得到k与b的值,进而确定出直线EF的解析式.
(2)设BF=a,由CB-FB表示出CF,由EF=ED+FB表示出EF,在直角三角形CEF中,利用勾股定理列出关于a的方程,求出方程的解得到a的值为10,可得出F为BC的三等分点;
(3)当CE=CF时,EF最短,此时△CEF为等腰直角三角形,由题意设出F(30,b),即FB=b,由CB-FB表示出CF,即为CE,由EF=BF+DE=2BF=2b,在直角三角形CEF中,由表示出的CF与CE利用勾股定理表示出EF,可列出关于b的方程,求出方程的解得到b的值,确定出E与F的坐标,设直线EF的解析式为y=kx+b,将E和F的坐标代入得到关于k与b的二元一次方程组,求出方程组的解得到k与b的值,进而确定出直线EF的解析式.
解答:(1)证明:延长ED至F′,使DF′=BF,
∵四边形ABCD是正方形,
∴AB=AD,∠ABF=∠ADF′=90°,
∴△ABF≌△ADF’(SAS),
∴AF=AF′,∠BAF=∠DAF′,
∵∠F′AE=∠F′AD+∠DAE=∠BAF+∠DAE=∠DAB-∠EAF=45°,
又∵∠EAF=45°,
∴∠F′AE=∠EAF,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′=ED+DF′=ED+BF;
(2)解:设BF=a,则CF=30-a,EF=ED+FB=15+a,
在Rt△CEF中,根据勾股定理得:EC2+CF2=EF2,
∴152+(30-a)2=(15+a)2,
∴a=10,
∴F为BC的三等分点,
∴F(30,10);
(3)解:当CE=CF时,EF最短,此时△CEF为等腰直角三角形,
设F坐标为(30,b),可得FB=b,
∴CF=CE=BC-FB=30-b,
∴EF=
(30-b),
又EF=FB+DE,∴
(30-b)=2b,
解得:b=
=30
-30,
∴FB=DE=30
-30,
∴E(30
-30,30),F(30,30
-30),
设直线EF的解析式为y=kx+b,
将E和F的坐标代入得:
,
解得:
,
则直线EF的解析式为y=-x+30
.
故答案为:y=-x+30
.
∵四边形ABCD是正方形,
∴AB=AD,∠ABF=∠ADF′=90°,
∴△ABF≌△ADF’(SAS),
∴AF=AF′,∠BAF=∠DAF′,
∵∠F′AE=∠F′AD+∠DAE=∠BAF+∠DAE=∠DAB-∠EAF=45°,
又∵∠EAF=45°,
∴∠F′AE=∠EAF,
|
∴△AEF≌△AEF′(SAS),
∴EF=EF′=ED+DF′=ED+BF;
(2)解:设BF=a,则CF=30-a,EF=ED+FB=15+a,
在Rt△CEF中,根据勾股定理得:EC2+CF2=EF2,
∴152+(30-a)2=(15+a)2,
∴a=10,
∴F为BC的三等分点,
∴F(30,10);
(3)解:当CE=CF时,EF最短,此时△CEF为等腰直角三角形,
设F坐标为(30,b),可得FB=b,
∴CF=CE=BC-FB=30-b,
∴EF=
| 2 |
又EF=FB+DE,∴
| 2 |
解得:b=
30
| ||
2+
|
| 2 |
∴FB=DE=30
| 2 |
∴E(30
| 2 |
| 2 |
设直线EF的解析式为y=kx+b,
将E和F的坐标代入得:
|
解得:
|
则直线EF的解析式为y=-x+30
| 2 |
故答案为:y=-x+30
| 2 |
点评:此题考查了一次函数综合题,涉及的知识有:全等三角形的判定与性质,坐标与图形性质,利用待定系数法求一次函数解析式,正方形的性质,等腰直角三角形的性质,以及勾股定理,利用了转化的数学思想,其中根据题意得到当CE=CF时,EF最短是解第三问的关键.

练习册系列答案
相关题目
 (2012•惠山区一模)如图,已知AB∥CD,∠AEF=80°,则∠DCF为
(2012•惠山区一模)如图,已知AB∥CD,∠AEF=80°,则∠DCF为