题目内容
如图,已知正方形ABCD的边长与Rt△EFG的直角边EF的长均为4cm,FG=8cm,AB与FG在同一条直线l上、开始时点F与点B重合,让Rt△EFG以每秒1cm速度在直线l上从右往左移动, 直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.
直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.(1)当x=2秒时,求y的值;
(2)求y与x之间的函数关系式,并写出自变量x的取值范围.
分析:(1)当x=2时,FB=2,根据FG的长可求出BG的值,利用△ECH∽△GBH所得比例线段即可求得BH的长,由于阴影部分是个直角梯形,根据梯形的面积公式即可求解.
(2)此题要根据F点的不位置分情况讨论,当F、A重合时,x=4,那么可分两种情况:
①0<x≤4时,此种情况与(1)题相同,可按照(1)题的方法,先求得BH的值,然后按梯形的面积公式求解;
②4<x≤8时,重合部分仍是直角梯形,只不过需要分两步求出AK、BH的长,方法同上.
(2)此题要根据F点的不位置分情况讨论,当F、A重合时,x=4,那么可分两种情况:
①0<x≤4时,此种情况与(1)题相同,可按照(1)题的方法,先求得BH的值,然后按梯形的面积公式求解;
②4<x≤8时,重合部分仍是直角梯形,只不过需要分两步求出AK、BH的长,方法同上.
解答: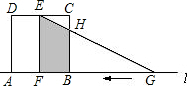 解:(1)当x=2时,如图,
解:(1)当x=2时,如图,
∵△ECH∽△GBH,
∴
=
=
=
,∴BH=3(2分)
∴y=
=7.(2分)(只要求得y=7可得4分)
(2)同理当0≤x≤4时,
=
=
=
,
∴BH=
,(1分)
∴y=
=-
x2+4x(0≤x≤4);(2分)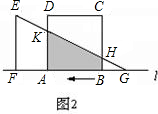
当4<x≤8时,如图,
仍有BH=
,
且
=
?
=
?KA=
.(1分)
∴y=
=20-2x(4<x≤8).(2分)
(各解析式(2分)、取值范围(1分);不等号写≤或<淡化要求,不扣分)
 解:(1)当x=2时,如图,
解:(1)当x=2时,如图,∵△ECH∽△GBH,
∴
| EC |
| BG |
| 2 |
| 6 |
| CH |
| BH |
| 4-BH |
| BH |
∴y=
| (3+4)×2 |
| 2 |
(2)同理当0≤x≤4时,
| EC |
| BG |
| x |
| 8-x |
| CH |
| BH |
| 4-BH |
| BH |
∴BH=
| 8-x |
| 2 |
∴y=
(
| ||
| 2 |
| 1 |
| 4 |

当4<x≤8时,如图,
仍有BH=
| 8-x |
| 2 |
且
| KA |
| EF |
| AG |
| FG |
| KA |
| 4 |
| 12-x |
| 8 |
| 12-x |
| 2 |
∴y=
(
| ||||
| 2 |
(各解析式(2分)、取值范围(1分);不等号写≤或<淡化要求,不扣分)
点评:此题主要考查了正方形的性质、相似三角形的判定和性质以及梯形面积的计算方法,同时还考查了分类讨论的数学思想,难度适中.

练习册系列答案
相关题目
 如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM.
如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM. (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( ) 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.