题目内容
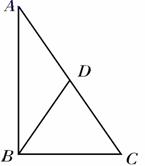
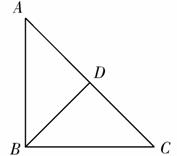
如图1,在△ABC中,∠ABC=90°,AB=BC,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°),得到△EFD,点A的对应点为点E,点B的对应点为点F,连接BE、CF.
(1)判断BE与CF的位置、数量关系,并说明理由;
(2)若连接BF、CE,请直接写出在旋转过程中四边形BEFC能形成哪些特殊四边形;
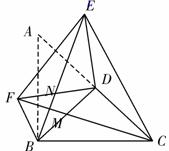
(3)如图2,将△ABC中AB=BC改成AB≠BC时,其他条件不变,直接写出α为多少度时(1)中的两个结论同时成立.
解:(1)FC=BE,FC⊥BE.
证明:∵∠ABC=90°,BD为斜边AC的中线,AB=BC,
∴BD=AD=CD.∠ADB=∠BDC=90°
∵△ABD旋转得到△EFD,∴∠EDB=∠FDC.
ED=BD,FD=CD.
∴△BED≌△CFD.
∴BE=CF.
∴∠DEB=∠DFC.
∵∠DNE=∠FNB,∴∠DEB+∠DNE=∠DFC+∠FNB.
∴∠FMN=∠NDE=90°
∴FC⊥BE.……
(2)等腰梯形和正方形.
(3)当α=90°(1)中的两个结论同时成立

练习册系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=