题目内容
【题目】如图，AD是△ABC的角平分线，以AD为弦的⊙O交AB、AC于E、F，已知EF∥BC．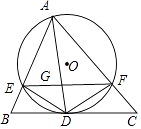
（1）求证：BC是⊙O的切线；
（2）若已知AE=12，CF=6，求DE的长．
【答案】
（1）
证明：连接OD，
∵AD是△ABC的角平分线，
∴∠1=∠2，
∴ 
= 
，
∴OD⊥EF，
∵EF∥BC，
∴OD⊥BC，
∴BC是⊙O的切线；
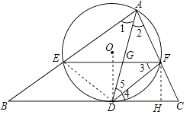
（2）
解：连接DE，
∵ = ，
∴DE=DF，
∵EF∥BC，
∴∠3=∠4，
∵∠1=∠3，
∴∠1=∠4，
∵∠DFC=∠AED，
∴△AED∽△DFC，
∴ 
= 
，即 
= 
，
∴DE2=72，
∴DE=6 
．
【解析】（1）连接OD，由角平分线的定义得到∠1=∠2，得到 = ，根据垂径定理得到OD⊥EF，根据平行线的性质得到OD⊥BC，于是得到结论；（2）连接DE，由 = ，得到DE=DF，根据平行线的性质得到∠3=∠4，等量代换得到∠1=∠4，根据相似三角形的性质即可得到结论；
练习册系列答案
相关题目
【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况，现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本．体育成绩分为四个等次：优秀、良好、及格、不及格．
体育锻炼时间 | 人数 |
4≤x≤6 |
|
2≤x＜4 | 43 |
0≤x＜2 | 15 |
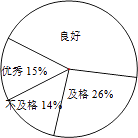
（1）试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数；
（2）统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表（如图表所示），请将图表填写完整（记学生课外体育锻炼时间为x小时）；
（3）全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”，请估计这些学生中课外体育锻炼时间不少于4小时的学生人数．
