题目内容
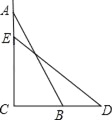
【题目】如图，在△ABC中，AB＝AC，D，A，E三点都在直线m上，∠BDA＝∠AEC＝∠BAC，BD＝3，CE＝6，则DE的长为______.
【答案】9
【解析】
由∠ABD+∠BAD+∠BDA=180°，∠CAE+∠BAD+∠BAC=180°，∠BDA=∠BAC可得∠ABD=∠CAE，结合AB=AC，∠BDA=∠AEC可得△ADB≌△CEA，由此可得AD=CE=6，AE=BD=3，从而可得DE=AD+AE=9.
∵∠ABD+∠BAD+∠BDA=180°，∠CAE+∠BAD+∠BAC=180°，∠BDA=∠BAC，
∴∠ABD=∠CAE，
又∵AB=AC，∠BDA=∠AEC，
∴△ADB≌△CEA，
∴AD=CE=6，AE=BD=3，
∴DE=AD+AE=9.
故答案为：9.
练习册系列答案
初中学业考试导与练系列答案
相关题目
