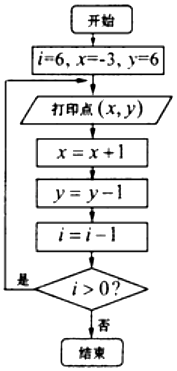
题目内容
【题目】小明在某次作业中得到如下结果: sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°≈( ![]() )2+(
)2+( ![]() )2=1.
)2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
【答案】解:(Ⅰ)当α=30°时, sin2α+sin2(90°﹣α)
=sin230°+sin260°
=( ![]() )2+(
)2+( ![]() )2
)2
= ![]() +
+ ![]()
=1;
(Ⅱ)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=( ![]() )2+(
)2+( ![]() )2
)2
= ![]()
= ![]()
=1.
【解析】(1)将α=30°代入,根据三角函数值计算可得;(2)设∠A=α,则∠B=90°﹣α,根据正弦函数的定义及勾股定理即可验证.
【考点精析】本题主要考查了互余两角的三角函数关系和特殊角的三角函数值的相关知识点,需要掌握互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能正确解答此题.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案【题目】为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动,某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |

(1)表中a= , b=;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.