题目内容
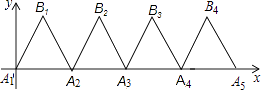
【题目】如图,在平面直角坐标系中,四边形ABCD的边AD在x轴上,点C在y轴的负半轴上,直线BC∥AD,且BC=3,OD=2,将经过A、B两点的直线l:y=﹣2x﹣10向右平移,平移后的直线与x轴交于点E,与直线BC交于点F,设AE的长为t(t≥0).
(1)四边形ABCD的面积为;
(2)设四边形ABCD被直线l扫过的面积(阴影部分)为S,请直接写出S关于t的函数解析式;
(3)当t=2时,直线EF上有一动点,作PM⊥直线BC于点M,交x轴于点N,将△PMF沿直线EF折叠得到△PTF,探究:是否存在点P,使点T恰好落在坐标轴上?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)20
(2)
解:①当0≤t≤3时,∵BC∥AD,AB∥EF,
∴四边形ABFE是平行四边形,
∴S=AEOC=4t;
②当3≤t<7时,如图1,
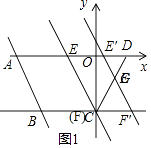
∵C(0,﹣4),D(2,0),
∴直线CD的解析式为:y=2x﹣4,
∵E′F′∥AB,BF′∥AE′
∴BF′=AE=t,
∴F′(t﹣3,﹣4),
直线E′F′的解析式为:y=﹣2x+2t﹣10,
解 ![]() 得,
得, 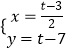
∴G( ![]() ,t﹣7),
,t﹣7),
∴S=S四边形ABCD﹣S△DE′G=20﹣ ![]() ×(7﹣t)×(7﹣t)=﹣
×(7﹣t)×(7﹣t)=﹣ ![]() t2+7t﹣
t2+7t﹣ ![]() ,
,
③当t≥7时,S=S四边形ABCD=20,
综上所述:S关于t的函数解析式为:S= 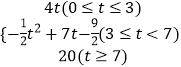 ;
;
(3)
解:当t=2时,点E,F的坐标分别为(﹣3,0),(﹣1,﹣4),
此时直线EF的解析式为:y=﹣2x﹣6,
设动点P的直线为(m,﹣2m﹣6),
∵PM⊥直线BC于M,交x轴于n,
∴M(m,﹣4),N(m,0),
∴PM=|(﹣2m﹣6)﹣(﹣4)|=2|m+1|,PN=(﹣2m﹣6|=2(m+3|,FM=|m﹣(﹣1)|=|m+1,
①假设直线EF上存在点P,使点T恰好落在x轴上,
如图2,连接PT,FT,则△PFM≌△PFT,
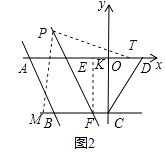
∴PT=PM=2|m+1|,FT=FM=|m+1|,∴ ![]() =2,
=2,
作FK⊥x轴于K,则KF=4,
由△TKF∽△PNT得, ![]() =2,
=2,
∴NT=2KF=8,
∵PN2+NT2=PT2,
∴4(m+3)2+82=4(m+1)2,
解得:m=﹣6,∴﹣2m﹣6=﹣6,
此时,P(﹣6,6);
②假设直线EF上存在点P,使点T恰好落在y轴上,
如图3,连接PT,FT,则△PFM≌△PFT,
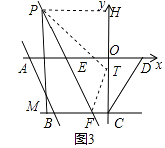
∴PT=PM=2|m+1|,FT=FM=|m+1|,
∴ ![]() =2,
=2,
作PH⊥y轴于H,则PH=|m|,
由△TFC∽△PTH得, ![]() ,
,
∴HT=2CF=2,
∵HT2+PH2=PT2,
即22+m2=4(m+1)2,
解得:m=﹣ ![]() ,m=0(不合题意,舍去),
,m=0(不合题意,舍去),
∴m=﹣ ![]() 时,﹣2m﹣6=﹣
时,﹣2m﹣6=﹣ ![]() ,
,
∴P(﹣ ![]() ,﹣
,﹣ ![]() ),
),
综上所述:直线EF上存在点P(﹣6,6)或P(﹣ ![]() ,﹣
,﹣ ![]() )使点T恰好落在y轴上.
)使点T恰好落在y轴上.
【解析】解:(1)在y=﹣2x﹣10中,当y=0时,x=﹣5,
∴A(﹣5,0),
∴OA=5,
∴AC=7,
把x=﹣3代入y=﹣2x﹣10得,y=﹣4
∴OC=4,
∴四边形ABCD的面积= ![]() (3+7)×4=20;
(3+7)×4=20;
所以答案是:20;
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份 | 2014 | 2015 | 2016 | 2017(预计) |
快递件总量(亿件) | 140 | 207 | 310 | 450 |
电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?