题目内容
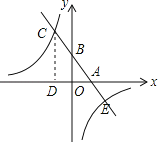
【题目】如图,已知一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=![]() (a≠0)的图象在第二象限交于点C,CD⊥x轴垂足为D点,若OB=2OA=3OD=6.
(a≠0)的图象在第二象限交于点C,CD⊥x轴垂足为D点,若OB=2OA=3OD=6.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)直接写出关于x的不等式![]() >kx+b的解集.
>kx+b的解集.
【答案】(1)y=﹣2x+6,![]() ;(2)﹣2<x<0或x>5.
;(2)﹣2<x<0或x>5.
【解析】
(1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.
(2)两个函数的解析式作为方程组,解方程组即可求得另一个交点的坐标,然后根据图象一次函数的图象在反比例函数图象的下方,即可解决问题.
(1)∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∴A(3,0),B(0,6),
∵CD⊥OA,
∴DC∥OB,
∴![]() ,即
,即![]() ,
,
∴CD=10,
∴点C坐标(﹣2,10),
把A(3,0),B(0,6)代入y=kx+b得![]()
解得![]() ,
,
∴一次函数为y=﹣2x+6.
∵反比例函数y=![]() (a≠0)的图象经过点C(﹣2,10),
(a≠0)的图象经过点C(﹣2,10),
∴a=﹣2×10=﹣20,
∴反比例函数解析式为y=﹣![]() .
.
(2)由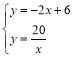 解得
解得![]() 或
或![]() ,
,
故另一个交点坐标为(5,﹣4).
由图象可知不等式![]() >kx+b的解集:﹣2<x<0或x>5.
>kx+b的解集:﹣2<x<0或x>5.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】我市某乡镇在农业产业合作化销售中,其中一农产品经分析发现月销售量y(万件)与月份x(月)的关系为: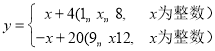 ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 |
(1)请你根据表格求出每件产品利润(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?