题目内容
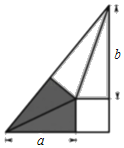
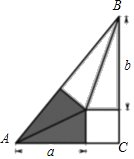
【题目】我国古代伟大的数学家刘微将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形．后人借助这种分割方法所得的图形证明了勾股定理，如图所示若a＝3，b＝4，则该三角形的面积为（ ）
A. 10B. 12C. 
D. 
【答案】B
【解析】
设小正方形的边长为x，在直角三角形ACB中，利用勾股定理可建立关于x的方程，利用整体代入的思想解决问题，进而可求出该三角形的面积．
解：设小正方形的边长为x，
∵a＝3，b＝4，
∴AB＝3+4＝7，
在Rt△ABC中，AC2+BC2＝AB2，
即（3+x）2+（x+4）2＝72，
整理得，x2+7x﹣12＝0，
而长方形面积为x2+7x+12＝12+12＝24
∴该三角形的面积为12，
故选：B．
练习册系列答案
孟建平名校考卷系列答案
相关题目
【题目】某校团委组织“阳光助残”献爱心捐款活动，九年级（2）班学生捐款如表：
捐款金额（元） | 5 | 10 | 15 | 20 |
人数（人） | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是（ ）
A. 10元，15元 B. 15元，15元 C. 10元，20元 D. 16元，17元
