题目内容
【题目】我市某乡镇在农业产业合作化销售中,其中一农产品经分析发现月销售量y(万件)与月份x(月)的关系为: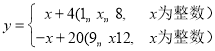 ,每件产品的利润z(元)与月份x(月)的关系如下表:
,每件产品的利润z(元)与月份x(月)的关系如下表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 |
(1)请你根据表格求出每件产品利润(元)与月份x(月)的关系式;
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润(万元)与月份x(月)的关系式;
(3)当x为何值时,月利润w有最大值,最大值为多少?
【答案】(1) z=﹣x+20; (2) 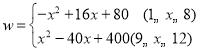 (x均为整数)(3)当x=8时,w取最大值,最大值为144万元
(x均为整数)(3)当x=8时,w取最大值,最大值为144万元
【解析】
本题是通过构建函数模型解答销售利润的问题.依据题意易得出每件产品利润(元)与月份x(月)的关系式,然后根据销售利润=销售量×(售价﹣进价),列出平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式,再依据函数的增减性求得最大利润.
(1)依题意,设每件产品利润(元)与月份x(月)的关系式为:z=kx+b,由表中的数据有
![]() ,解得
,解得![]() ,
,
故每件产品利润(元)与月份x(月)的关系式为:z=﹣x+20
(2)依题意,
当1≤x≤8时,w=zy=(20﹣x)(x+4)=﹣x2+16x+80
当9≤x≤12时,w=zy=(20﹣x)(﹣x+20)=x2﹣40x+400
∴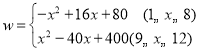 (x均为整数)
(x均为整数)
(3)由(2)得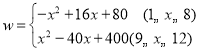 (x均为整数)
(x均为整数)
当1≤x≤8时,对称轴为x=![]() =8
=8
∴当x=8时,w取最大值,最大值为144
当9≤x≤12时,对称轴为x=![]() =20
=20
∴当x=9时,w取最大值,最大值为121
∴当x=8时,w取最大值,最大值为144万元

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.