题目内容
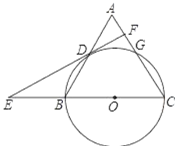
【题目】如图,在△ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论:①DF⊥AC;②DO=DB;③cos∠E=![]() .正确的是__.
.正确的是__.
【答案】①③
【解析】
首先连接OD,由CA=CB,OB=OD,易证得OD∥AC,又由DF是O的切线,即可证得①;首先连接BG,CD,可求得CD的长,然后由ABCD=2S△ABC=AC×BG,求得BG的长,易证得BG∥EF,即可得cos∠E =cos∠CBG=![]() 即可得出③
即可得出③
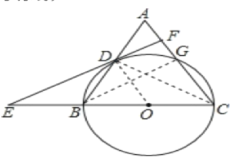
证明:连接OD,
∴CA=CB,OB=OD,
∴∠A=∠ABC,∠ABC=∠ODB,
∴∠A=∠ODB
∴OD∥AC
∵DF是O的切线,
∴OD⊥DF
∴DF⊥AC.故①正确
连接BG,CD
∵BC是直径,
∴∠BDC=90°,
∵CA=CB=10
∴AD= BD=![]() AB=
AB=![]() =6
=6
CD=![]()
∵AB·CD =2S△ABC=AC·BG,
∴BG=![]()
∵BG⊥AC,DF⊥AC
∴BG∥EF,
∴∠E=∠CBG,
∴cos∠E=cos∠CBG=![]() ,
,
∴③正确
故答案为:①③

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目