题目内容
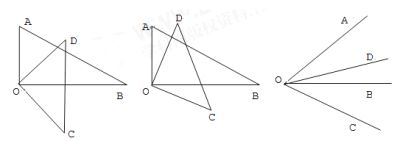
【题目】(1) 将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起, ∠AOB=∠DOC=90°.
①如图(1),若OD是∠AOB的平分线时,求∠BOD和∠AOC的度数.
②如图(2),若OD不是∠AOB的平分线,试猜想∠AOC与∠BOD的数量关系,并说明理由.
(2)如图(3),如果两个角∠AOB = ∠DOC= m°(0< m <90),直接写出∠AOC与∠BOD的数量关系.
【答案】(1)①45°;135°;②∠AOC+∠BOD=180°,理由见解析;(2)∠AOC+∠BOD=2 m° .
【解析】
(1)先根据角平分线的定义求出∠BOD,再求出∠BOC,然后根据∠AOC=∠AOB+∠BOC计算即可;
(2)根据∠BOC=∠DOC-∠BOD,∠AOC=∠AOB+∠BOC,整理即可得出答案;
(3)与(2)的步骤类似求解即可.
解: (1) ①因为∠AOB=90°, OD平分∠AOB,
所以![]() .
.
因为∠DOC=90° , ∠BOD=45°,
所以∠BOC=∠DOC-∠BOD=90°-45°=45°.
因为∠AOC=∠AOB+∠BOC,
所以∠AOC=90°+45°=135°;
②数量关系: ∠AOC+∠BOD=180°,
理由:∵∠BOC=∠DOC-∠BOD= 90°-∠BOD,
∠AOC=∠AOB+∠BOC,
∴∠AOC =90°+90°-∠BOD,
∴∠AOC+∠BOD=180° ;
(2) 关系: ∠AOC+∠BOD=2 m°.
理由:∵∠BOC=∠DOC-∠BOD= m°-∠BOD,
∠AOC=∠AOB+∠BOC,
∴∠AOC =m°+m°-∠BOD,
∴∠AOC+∠BOD=2m° ;

练习册系列答案
相关题目