题目内容
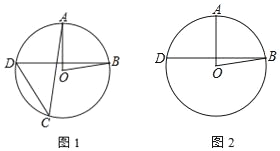
【题目】已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为![]() ,过点C作⊙A的切线交x轴于点B(-4,0).
,过点C作⊙A的切线交x轴于点B(-4,0).
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.

【答案】(1)![]() ;(2)G(
;(2)G(![]() ,
,![]() +2 ).
+2 ).
【解析】
(1)连接AC,由于BC与⊙A相切,则AC⊥BC,在Rt△ABC中,OC⊥AB,根据射影定理即可求得OC的长,从而得到C点的坐标,进而用待定系数法求出直线BC的解析式.
(2)可设出G点的坐标(设横坐标,利用直线BC的解析式表示纵坐标),连接AP、AG;由于GC、GP都是⊙A的切线,那么∠AGC=∠ABP=60°,在Rt△AGC中,AC的长易求得,根据∠AGC的度数,即可求得AG的长;过G作GH⊥x轴于H,在Rt△GAH中,可根据G点的坐标表示出AH、GH的长,进而由勾股定理求得G点的坐标.
解:(1)如图1所示,连接AC,则AC=![]() .
.
在Rt△AOC中,AC=![]() ,OA=1,则OC=2,
,OA=1,则OC=2,
∴点C的坐标为(0,2).
设切线BC的解析式为y=kx+b,
它过点C(0,2),B(﹣4,0),
则有![]() ,
,
解之得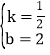 ,
,
∴![]() ;
;
(2)如图1所示,设点G的坐标为(a,c),
∵点G在直线y=![]() x+2上,
x+2上,
∴c=![]() a+2,
a+2,
过点G作GH⊥x轴,垂足为H点,则OH=a,GH=c=![]() a+2,连接AP,AG.
a+2,连接AP,AG.
∵AC=AP,AG=AG,所以Rt△ACG≌Rt△APG (HL),
∴∠AGC=![]() ×120°=60°.
×120°=60°.
在Rt△ACG中,
∵∠AGC=60°,AC=![]() ,
,
∴sin60°=![]() ,
,
∴AG=![]() .
.
在Rt△AGH中,AH=OH﹣OA=a﹣1,GH=![]() a+2,
a+2,
∵AH2+GH2=AG2,
∴(a﹣1)2+![]() =
=![]() ,
,
解之得:a1=![]() ,a2=﹣
,a2=﹣![]() (舍去),
(舍去),
点G的坐标为(![]() ,
,![]() +2 ).
+2 ).