题目内容
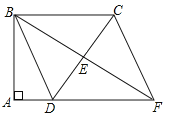
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
【答案】(1)证明见试题解析;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)由平行线的性质和中点的性质证明三角形全等,然后由对角线互相平分的四边形是平行四边形完成证明;
(2)由等腰三角形的性质,分三种情况:①BD=BC,②BD=CD,③BC=CD,分别求四边形的面积.
试题解析:(1)∵∠A=∠ABC=90°,∴BC∥AD,∴∠CBE=∠DFE,在△BEC与△FED中,∵∠CBE=∠DFE,∠BEC=∠FED,CE=DE,∴△BEC≌△FED,∴BE=FE,又∵E是边CD的中点,∴CE=DE,∴四边形BDFC是平行四边形;
(2)①BC=BD=3时,由勾股定理得,AB=![]() =
=![]() =
=![]() ,所以,四边形BDFC的面积=
,所以,四边形BDFC的面积=![]() =
=![]() ;
;
②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG=![]() =
=![]() =
=![]() ,所以,四边形BDFC的面积=
,所以,四边形BDFC的面积=![]() =
=![]() ;
;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;
综上所述,四边形BDFC的面积是![]() 或
或![]() .
.


【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
