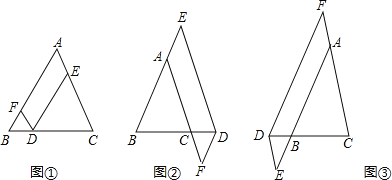äãá¢áÖàï
Àƒäãá¢À¢ØîøˆÈ˜çÐOòúçàÝÔÀ¼ABCáÖçáàöØ£çÐȘ꘧ÆOAȘOBȘOCÈÛ
È´1ÈˋàÓë¥1ȘØîøˆÀüAOB=150ÀÐȘÀüBOC=120ÀÐȘ§¨À¼BOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼ADCÈÛ
ÂìÀüDAOçáÑàò»òúÑÁèìÈ¢
ÂÖÆûçàò§ÝÚòƒüÔÑöOAȘOBȘOCøÛ¥ðçáò»ê¢¿ÄüçȘýÂøÊû¼È£
È´2ÈˋèÒÀüAOB=ÎêȘÀüBOC=ÎôÈÛ
ÂìçÝÎêȘÎôôºæÐòýûÇ¿ÄüçòÝȘOA+OB+OCÆÅæŸÅÀøçÈ¢úŠåÖë¥2øÅ£Ù°—ñ«¤üä¾¥±çáë¥ÅöȘýÂùçû¼âÚÆèÈ£
ÂÖà¶çàÝÔÀ¼ABCçáÝÔ°Êöˆ1ȘøݧÆÅÇ°—OA+OB+OCçáæŸÅÀøçÈÛ
ÀƒÇÞ¯¡À¢
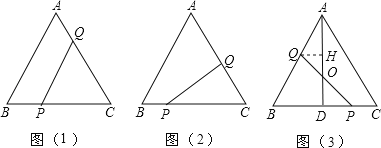
È´1Èˋ
§ãȤÂìÀüAOB=150ÀÐȘÀüBOC=120ÀÐȘ
ÀÁÀüAOC=360ÀÐˋ120ÀÐˋ150ÀÐ=90ÀÐȘ
ÀÔ§¨À¼BOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼ADCȘ
ÀÁÀüOCD=60ÀÐȘÀüD=ÀüBOC=120ÀÐȘ
ÀÁÀüDAO=360ÀÐˋÀüAOCˋÀüOCDˋÀüD=90ÀÐȘ
¿òÇÞ¯¡öˆÈ¤90ÀÐÈ£
ÂÖüÔÑöOAȘOBȘOCøÛ¥ðçáò»ê¢¿ÄüçòúOA2+OB2=OC2Ș
àÓë¥1Ș꘧ÆODȘ
ÀÔÀ¼BOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼ADCȘ
ÀÁÀ¼ADCÀíÀ¼BOCȘÀüOCD=60ÀÐȘ
ÀÁCD=OCȘÀüADC=ÀüBOC=120ÀÐȘAD=OBȘ
ÀÁÀ¼OCDòúçàÝÔ໧úÅöȘ
ÀÁOC=OD=CDȘÀüCOD=ÀüCDO=60ÀÐȘ
ÀÔÀüAOB=150ÀÐȘÀüBOC=120ÀÐȘ
ÀÁÀüAOC=90ÀÐȘ
ÀÁÀüAOD=30ÀÐȘÀüADO=60ÀÐȘ
ÀÁÀüDAO=90ÀÐȘ
åÖRtÀ¼ADOøÅȘÀüDAO=90ÀÐȘ
ÀÁOA2+OB2=OD2Ș
ÀÁOA2+OB2=OC2
È´2Èˋ
§ãȤÂìçÝÎê=Îô=120ÀÐòÝȘOA+OB+OCÆÅæŸÅÀøçÈÛ
àÓë¥2Ș§¨À¼AOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼AÀðOÀðCȘ꘧ÆOOÀðȘ
ÀÁÀ¼AÀðOÀðCÀíÀ¼AOCȘÀüOCOÀð=ÀüACAÀð=60ÀÐȘ
ÀÁOÀðC=OCȘOÀðAÀð=OAȘAÀðC=BCȘ
ÀüAÀðOÀðC=ÀüAOCÈÛ
ÀÁÀ¼OC OÀðòúçàÝÔ໧úÅöȘ
ÀÁOC=OÀðC=OOÀðȘÀüCOOÀð=ÀüCOÀðO=60ÀÐȘ
ÀÔÀüAOB=ÀüBOC=120ÀÐȘ
ÀÁÀüAOC=ÀüAÀðOÀðC=120ÀÐȘ
ÀÁÀüBOOÀð=ÀüOOÀðAÀð=180ÀÐȘ
ÀÁùáçÐBȘOȘOÀðȘAÀð¿ýüÔȘ
ÀÁOA+OB+OC=OÀðAÀð+OB+OOÀð=BAÀðòÝøçæŸÅÀÈ£
ÂÖÀÔÀüAOB=ÀüBOC=120ÀÐȘ
ÀÁÀüAOC=120ÀÐȘ
ÀÁOöˆÀ¼ABCçáøÅÅáȘ
ÀÔùáçÐBȘOȘOÀðȘAÀð¿ýüÔȘ
ÀÁBDÀëACȘ
ÀÔ§¨À¼AOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼AÀðOÀðCȘ
ÀÁAÀðC=AC=BCȘ
ÀÁAÀðB=2BDȘ
åÖRtÀ¼BCDøÅȘBD= ![]() BC=
BC= ![]() Ș
Ș
ÀÁAÀðB= ![]() Ș
Ș
ÀÁçÝçàÝÔÀ¼ABCçáÝÔ°Êöˆ1òÝȘOA+OB+OCçáæŸÅÀøçAÀðB= ![]() ÈÛ
ÈÛ

Àƒ§ãö—À¢È´1ÈˋÂ졪ƒïøɧúçáÑ´ØÍçûç§ÀüAOC=360ÀÐˋ120ÀÐˋ150ÀÐ=90ÀÐȘÆèÆÖ§¨À¼BOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼ADCȘÆÖòúçûç§ÀüOCD=60ÀÐȘÀüD=ÀüBOC=120ÀÐȘ¡ªƒïùáÝÔÅöçááÖ§ú¤ë¥Ç¢èçû秧ÃôÜÈ£ÂÖàÓë¥1Ș꘧ÆODȘÆèÆÖÀ¼BOCàóçÐC¯Çù°òÝíŠñ§ü·Å»æˆ60ÀÐçûÀ¼ADCȘçûç§À¼ADCÀíÀ¼BOCȘÀüOCD=60ÀÐȘ¡ªƒïà¨çà໧úÅöçáÅåøòçûç§CD=OCȘÀüADC=ÀüBOC=120ÀÐȘAD=OBȘëó°—À¼OCDòúçàÝÔ໧úÅöȘ¡ªƒïçàÝÔ໧úÅöçáÅåøòçûç§OC=OD=CDȘÀüCOD=ÀüCDO=60ÀÐȘÆèÆÖÀüAOB=150ÀÐȘÀüBOC=120ÀÐȘçûç§ÀüAOC=90ÀÐȘúµçûÀüAOD=30ÀÐȘÀüADO=60ÀÐȘ¡ªƒï¿Ç¿èÑ´âڥǢèçû秧ÃôÜȣȴ2ÈˋÂìàÓë¥2ȘÆèÅ»æˆçáÅåøòçûç§OÀðC=OCȘOÀðAÀð=OAȘAÀðC=BCȘÀüAÀðOÀðC=ÀüAOCÈÛÈÛëó°—À¼OC OÀðòúçàÝÔ໧úÅöȘ¡ªƒïçàÝÔ໧úÅöçáÅåøòçûç§OC=OÀðC=OOÀðȘÀüCOOÀð=ÀüCOÀðO=60ÀÐȘÆèÆÖÀüAOB=ÀüBOC=120ÀÐȘçûç§ÀüAOC=ÀüAÀðOÀðC=120ÀÐȘëó°—ùáçÐBȘOȘOÀðȘAÀð¿ýüÔȘ¥Ç¢èçû秧ÃôÜȘÂÖ¡ªƒïÂìçá§ÃôܥǢèçû秧ÿ«ÈÛ

Àƒäãá¢À¢á°Åȃéáõ¥Ñꧡ—¯ÁȘ¡¼îÀéè![]() û«îÏèºýö¥ÆîÏÅȃìÅÅçáÀ¯¤¤æøä»ÅÇÀÝǵà■åÊà■Ș¡¼ýöà■îÀòøçá°è¥´àÓüôȤ
û«îÏèºýö¥ÆîÏÅȃìÅÅçáÀ¯¤¤æøä»ÅÇÀÝǵà■åÊà■Ș¡¼ýöà■îÀòøçá°è¥´àÓüôȤ
![]() ¯ÁȤ
¯ÁȤ![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]()
![]() ¯ÁȤ
¯ÁȤ![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]()
ë´¿»í«âÚȘçûç§ò»ƒïñøö—ÝÚàÓüôȤ
¯Á¥Ñ | 柡Ôñø | 󧃪ñø | øÅö£ò» | øÖò» | ñ§ýŸ |
|
|
|
|
|
|
|
|
|
|
|
|
![]() øݧÆÅÇ°—ÝÚøÅ
øݧÆÅÇ°—ÝÚøÅ![]() ÀÂ
ÀÂ![]() ÀÂ
ÀÂ![]() çáøçÈ£
çáøçÈ£
![]() Øâƒïò»ƒïñøö—ÝÚȘÆÅàùùçȤÀ¯æŸ¡ÔñøåÖ
Øâƒïò»ƒïñøö—ÝÚȘÆÅàùùçȤÀ¯æŸ¡ÔñøåÖ![]() ¯ÁȘ
¯ÁȘ![]() ¯Áçá°è¥´Ýà
¯Áçá°è¥´Ýà![]() ¯Á¤ûÀÝȘç¨ØýÆÅàùùç
¯Á¤ûÀÝȘç¨ØýÆÅàùùç![]() ¯Áçá°è¥´Øˆ¤ûȘúŠ¡½°—ê§ä¾øÏ°ø
¯Áçá°è¥´Øˆ¤ûȘúŠ¡½°—ê§ä¾øÏ°ø![]() ¯Á°è¥´¤ûçáâÚÆèÈÛ
¯Á°è¥´¤ûçáâÚÆèÈÛ
Àƒäãá¢À¢öˆôºæÐë˜îÏûú¢öëãåáÑêçáÅÒúµÈ˜á°øÅîÏë¥òÕ¿ïü·°—¯ÌèÓÆò¿¤¢óóíüçêÅë¥òÕȘû¢ÝƒòÕçË¥Üöˆ16åˆÈ˜òÕçá¥ÜúÛ¤ëÆòñîòúë´¿»Æòƒø£Ð¢ŸÈ˜üÁ¿ÄçáòÕ¥ÜíÜ¢ÜÀÂÆòñî¤ë£Ð¢Ÿçá£ÐñîàÓüôÝÚùªòƒÈ´æÉñîÆû=æÉòÕ¥Ü+æÉÆòñî+æÉ£ÐñîÈˋ
¿¤òÕò»ê¢ | íÜ¢Ü | Æòñî | £Ðñî |
ý£°˜¿»10݃ | ƒéíÜ | 6åˆ | û¢100刣ТŸÅÒ£Ðñî1åˆ È´£Ð¢Ÿý£æÐ100åˆòݯÇ100刣ТŸòí£ÐñîÈˋ |
°˜¿»10݃ | ¯ùíÜ | æÉòÕ¥Üçá10% | û¢100刣ТŸÅÒ£Ðñî1åˆ È´£Ð¢Ÿý£æÐ100åˆçáý¢ñøý£òí£ÐñîÈˋ |
È´1Èˋà¶Ø£ÇöÆò¿¤7݃Ș¿ýÅÒæÉñîÆûöˆÀÀ ÀÀåˆÈÛ
È´2ÈˋØîøˆîÏÅÈë¥òÕ¿ïÅÒ¿¤ë¥òÕçáæÉò»òú10çáí«ÝÑò»È˜úØ°˜¿»10݃ÈÛ
Âìà¶ñøÇöÆò¿¤È˜ñøÝޣТŸÈ˜û¢ÇöÆò¿¤10݃ȘæÉñîÆûöˆ1064åˆòÝȘ¿ýÆò¿¤êùÑÁ݃ë¥òÕÈ¢
ÂÖà¶áÐòúîÏÅÈë¥òտåÞàùȘÇƧÖå¥çá§úÑà°—ñÂȘåÖÀ¯û¢ÇöÆò¿¤10݃À¯ÆŠÀ¯Ø£ÇöÅåÆò¿¤ÀÝíãê§øøñ§ò§øÅîÀåþØ£øøȘáУÃîÀåþááØ£øøÈ¢¥óùÐýÂùçû¼âÚÆèÈÛ