题目内容
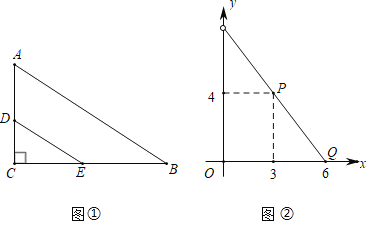
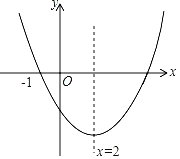
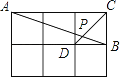
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2﹣9(其中a>0)上,AB∥x轴,点P是抛物线的顶点,tan∠PBA=2,∠BAC=45°.
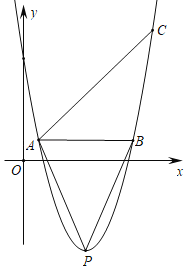
(1)填空:抛物线的顶点P的坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为10,当2m﹣3≤x≤2m+5时,y的最小值为5,求m的值.
【答案】(1)(m,﹣9);(2)S△ABC=![]() ;(3)m的值为﹣5﹣
;(3)m的值为﹣5﹣![]() 或3+
或3+![]() .
.
【解析】
(1)用配方法写出抛物线顶点式即求出顶点坐标;
(2)过P作AB的垂线PD,因为A、B具有对称性故点D为AB中点,构造∠PDB=90°,则把tan∠PBA=2转化为PD=2BD=AB.设AD=BD=n,进而用n表示A的坐标,再代入抛物线解析式,得到n与a的关系.过C作AB的垂线CE,构造等腰直角△ACE,设AE=CE=t,用t表示C的坐标并代入抛物线解析式,得到t与a的关系.最后直接AB与CE的积的一半即能用a表示△ABC的面积;
(3)利用△ABC面积求出a=1,抛物线开口向上,最小值为y=-9,故条件里提到的范围2m-3≤x≤2m+5不包含有对称轴x=m.分两种情况:①若此范围在对称轴左侧,即2m+5<m,y随x的增大而减小,所以x=2m+5时对应最小值;②若此范围在对称轴右侧,即2m-3>m,y随x的增大而增大,x=2m-3对应最小值.把相应的x和y值代入抛物线解析式即求得m的值.
(1)∵y=ax2﹣2amx+am2﹣9=a(x﹣m)2﹣9,
∴顶点P的坐标为(m,﹣9),
故答案为:(m,﹣9).
(2)过点P作PD⊥AB于点D,过点C作CE⊥AB于点E,
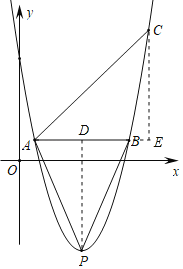
∵AB∥x轴,且点A、B在抛物线上,
∴PA=PB,
∴AD=BD
∵tan∠PBA=![]() =2,
=2,
∴PD=2BD=AB,
设AD=BD=n(n>0),则PD=AB=2n,
∴A(m﹣n,﹣9+2n),
把A的坐标代入抛物线解析式得:a(m﹣n﹣m)2﹣9=﹣9+2n,
整理得:n=![]() ,
,
∴AB=![]() ,A(m﹣
,A(m﹣![]() ,﹣9+
,﹣9+![]() ),
),
∵∠AEC=90°,∠BAC=45°,
∴AE=CE,
设AE=CE=t(t>0),则C(m﹣![]() +t,﹣9+
+t,﹣9+![]() +t),
+t),
把C的坐标代入抛物线解析式得:a(m﹣![]() +t﹣m)2﹣9=﹣9+
+t﹣m)2﹣9=﹣9+![]() +t,
+t,
整理得:t=![]() ,
,
∴CE=![]() ,
,
∴S△ABC=![]() ABCE=
ABCE=![]() ;
;
(3)∵S△ABC=![]() =10,a>0,
=10,a>0,
∴a=1,
∴抛物线解析式为:y=(x﹣m)2﹣9,
∴抛物线最小值y=﹣9<5,
∴当2m﹣3≤x≤2m+5时,不包含有对称轴x=m,
①若2m+5<m,即m<﹣5时,x=2m+5对应最小值y=5,
∴(2m+5﹣m)2﹣9=5,
解得:m1=﹣5+![]() (舍去),m2=﹣5﹣
(舍去),m2=﹣5﹣![]() ,
,
②若2m﹣3>m,即m>3时,x=2m﹣3对应最小值y=5,
∴(2m﹣3﹣m)2﹣9=5,
解得:m1=3+![]() ,m2=3﹣
,m2=3﹣![]() (舍去),
(舍去),
综上所述,m的值为﹣5﹣![]() 或3+
或3+![]() .
.

【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
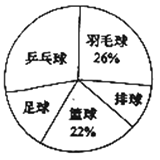
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.