题目内容
【题目】如图，反比例函数
（k＞0）与长方形OABC在第一象限相交于D，E两点，OA=2，OC=4，连结OD、OE、DE．记△OAD、△OCE的面积分别为
、
．当
=2时，求k的值及点D、E的坐标，试判断△ODE的形状．
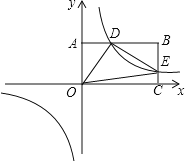
【答案】k=2，D（1，2），E（4，
），△ODE是直角三角形
【解析】
利用反比例函数k的几何意义，可求得k的值；然后可求得D、E的坐标，最后利用勾股定理的逆定理判断三角形的形状.
解：由反比例函数的性质得：S1=S2=
，则S1＋S2=k，则k=2.
∵S1=AO·AD=1，∴AD=1，即D（1，2）；
∵S2=OC·EC=1，∴EC=，即E（4，）.
△ODE是直角三角形．理由如下：
∵OD2=AO2＋AD2=5，EO2=CO2＋CE2=16
，DE2=DB2＋BE2=11，
∴OD2＋DE2=OE2，∴∠ODE=90°，△ODE是直角三角形．
练习册系列答案
相关题目
