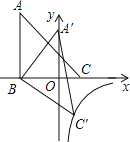
��Ŀ����
����Ŀ����֪�߳�Ϊ4��������ABCD������A������ԭ���غϣ�һ����������ͼ�������C������P��ÿ��1����λ�ٶȴӵ�A������AB�����˶�������Qͬʱ��ÿ��4����λ�ٶȴ�D������������εı�DC��CB��BA����˳ʱ�������˶�������P���Q����ʱֹͣ�˶������P���˶�ʱ��Ϊt��
��1������÷�������������ʽ��
��2������PD�����Ե�Q�������ε�ij����������ɵ������κ͡�PADȫ��ʱ�����Q�����ꣻ
��3���ú�t�Ĵ���ʽ��ʾ�Ե�Q��P��DΪ����������ε����s����ָ����Ӧt��ȡֵ��

���𰸡���1��y=![]() ��
��
��2��Q1��![]() ��4����Q2��4��
��4����Q2��4��![]() ����Q3��4��
����Q3��4��![]() ����
����
��3��s1=8t��0��t��1����s2=��2t2+2t+8��1��t��2����s3=��10t+24��2��t��![]() ����
����
��������
���⣨1������������ABCD�ı߳�Ϊ4���ɵ�C������Ϊ��4��4�������ô���ϵ���������������������ʽ��
��2���ֵ�Q��CD��BC��AB���ϣ�����ȫ�������ε��ж���������õ�Q�����ꣻ
��3���ֵ�Q��CD��BC��AB���ϣ��������������ʽ�����ͼ�ε�������㼴����⣮
����������⣺��1����������ABCD�ı߳�Ϊ4��
��C��������4��4����
�跴��������ʽΪy=![]() ��
��
��C������������ʽ�ã�k=16����������ʽΪy=![]() ��
��
��2����Q��DC��ʱ����ͼ��ʾ��
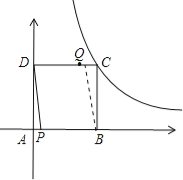
��ʱ��APD�ա�CQB��
��AP=CQ����t=4��4t�����t=![]() ��
��
��DQ=4t=![]() ����Q1��
����Q1��![]() ��4����
��4����
��Q��BC����ʱ��������λ�ã���ͼ��ʾ��

��Q���ϱߣ�����QCD�ա�PAD��
��AP=QC����4t��4=t�����t=![]() ��
��
��QB=8��4t=![]() ����ʱQ2��4��
����ʱQ2��4��![]() ����
����
��Q���±ߣ�����APD�ա�BQA��
��AP=BQ����8��4t=t�����t=![]() ��
��
��QB=![]() ����Q3��4��
����Q3��4��![]() ����
����
��Q��AB����ʱ����ͼ��ʾ��
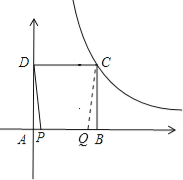
��ʱ��APD�ա�QBC��
��AP=BQ����4t��8=t�����t=![]() ��
��
��Ϊ0��t��![]() ��������ȥ��
��������ȥ��
��������Q1��![]() ��4���� Q2��4��
��4���� Q2��4��![]() ����Q3��4��
����Q3��4��![]() ����
����
��3����0��t��1ʱ��Q��DC�ϣ�DQ=4t����s=![]() ��4t��4=8t��
��4t��4=8t��
��1��t��2ʱ��Q��BC�ϣ���BP=4��t��CQ=4t��4��AP=t��
��s=S������ABCD��S��APD��S��BPQ��S��CDQ=16��![]() APAD��
APAD��![]() PBBQ��
PBBQ��![]() DCCQ=16��
DCCQ=16��![]() t��4��
t��4��![]() ��4��t��[4����4t��4��]��
��4��t��[4����4t��4��]��![]() ��4��4t��4���T��2t2+2t+8��
��4��4t��4���T��2t2+2t+8��
��2��t��![]() ʱ��Q��AB�ϣ�PQ=12��5t����s=
ʱ��Q��AB�ϣ�PQ=12��5t����s=![]() ��4����12��5t������s=��10t+24��
��4����12��5t������s=��10t+24��
��֮��s1=8t��0��t��1����
s2=��2t2+2t+8��1��t��2����
s3=��10t+24��2��t��![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�