题目内容
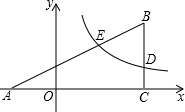
如图,在同一直角坐标系中,正比例函数y=kx与反比例函数y=
的图象分别交于第一、三象限的点B,D,已知点A(-a,O)、C(a,0).
(1)直接判断并填写:四边形ABCD的形状一定是______;
(2)①当点B为(p,2)时,四边形ABCD是矩形,试求p,k,和a的值;
②观察猜想:对①中的a值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能,直接写出B点的坐标;若不能,说明理由.

2
| ||
| x |
(1)直接判断并填写:四边形ABCD的形状一定是______;
(2)①当点B为(p,2)时,四边形ABCD是矩形,试求p,k,和a的值;
②观察猜想:对①中的a值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能,直接写出B点的坐标;若不能,说明理由.

(1)是平行四边形.
理由如下:
∵A(-a,0)、C(a,0),
∴OA=OC,
由对称性可知OB=OD,
∴四边形ABCD为平行四边形;
故答案为:平行四边形;
(2)①∵点B为(p,2),
∴
=2,
解得:p=
,
∴点B(
,2),
∴
k=2,
解得:k=
,
∵四边形ABCD是矩形,
∴AC=BD,OB=
AC,OC=
BD,
∴OB=OC,
∵OB=
=
,
∴a=
;
②对①中的a值,能使四边形ABCD为矩形的点B共有2个.
理由:当a=
时,点C的坐标为(
,0),点A的坐标为(-
,0),
若四边形ABCD是矩形,则有OB=OC=
,
设点B的坐标为(x,y),得:
,
解得:
或
(负值舍去),
∴点B的坐标为(
,2)或(2,
);
(3)四边形ABCD不能是菱形.
理由:若四边形ABCD是菱形,
则BD⊥AC,
∵点A、点C在x轴上,
∴直线BD与y轴重合,这与“双曲线y=
不与坐标轴相交”矛盾,
∴四边形ABCD不可能是菱形.
理由如下:
∵A(-a,0)、C(a,0),
∴OA=OC,
由对称性可知OB=OD,
∴四边形ABCD为平行四边形;
故答案为:平行四边形;
(2)①∵点B为(p,2),
∴
2
| ||
| p |
解得:p=
| 3 |
∴点B(
| 3 |
∴
| 3 |
解得:k=
2
| ||
| 3 |
∵四边形ABCD是矩形,
∴AC=BD,OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB=OC,
∵OB=
(
|
| 7 |
∴a=
| 7 |
②对①中的a值,能使四边形ABCD为矩形的点B共有2个.
理由:当a=
| 7 |
| 7 |
| 7 |
若四边形ABCD是矩形,则有OB=OC=
| 7 |
设点B的坐标为(x,y),得:
|
解得:
|
|
∴点B的坐标为(
| 3 |
| 3 |
(3)四边形ABCD不能是菱形.
理由:若四边形ABCD是菱形,
则BD⊥AC,
∵点A、点C在x轴上,
∴直线BD与y轴重合,这与“双曲线y=
2
| ||
| x |
∴四边形ABCD不可能是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目