题目内容
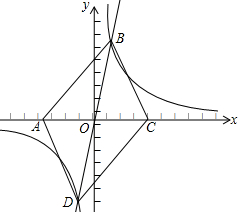
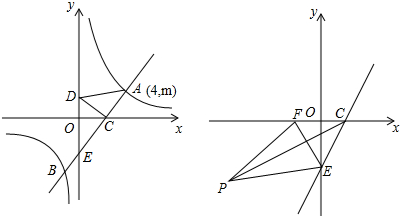
如图,直线y=kx+b交反比例函数y=
的图象于点A(4,m)和点B,交x轴于点C,交y轴于点E(0,-2
)
(1)求C点的坐标;
(2)在y轴上是否存在点D使CD=DA?若存在,求出D点的坐标;若不存在,说明理由;
(3)取C点关于y轴的对称点F,连EF,点P为△CEF外一点,连PE,PF,PC,当P在△CEF外运动时,若∠EPF=30°,有两个结论:①PE2+PF2=PC2②PE+PF=PC+EF,其中只有一个结论正确,作选择并证明.
8
| ||
| x |
| 3 |
(1)求C点的坐标;
(2)在y轴上是否存在点D使CD=DA?若存在,求出D点的坐标;若不存在,说明理由;
(3)取C点关于y轴的对称点F,连EF,点P为△CEF外一点,连PE,PF,PC,当P在△CEF外运动时,若∠EPF=30°,有两个结论:①PE2+PF2=PC2②PE+PF=PC+EF,其中只有一个结论正确,作选择并证明.

(1)∵点A(4,m)在反比例函数y=
的图象上,
∴m=
=2
,
∴点A的坐标为(4,2
),
∵点A(4,2
),点E(0,-2
)都在直线y=kx+b上,
∴
,
解得
,
∴直线解析式为y=
x-2
,
令y=0,则
x-2
=0,
解得x=2,
∴点C的坐标为(2,0);
(2)y轴上存在点D(0,2
),使CD=DA.
理由如下:设点D的坐标为(0,y),
则CD=
,
AD=
,
∵CD=DA,
∴
=
,
两边平方并整理得,4
y-24=0,
解得y=2
,
∴y轴上存在点D(0,2
),使CD=DA;
(3)结论①PE2+PF2=PC2正确.
理由如下:∵点C坐标为(2,0),点E坐标为(0,-2
),
∴CE=
=
=4,tan∠ECO=
=
=
,
∴∠ECO=60°,
又∵点F、C关于y轴对称,
∴FC=2+2=4,
∴FC=CE,
∴△CEF是等边三角形,
如图,把△PCE绕点C顺时针旋转60°得到△P′C′E,连接PP′,
则点E与点F重合,△PP′C为等边三角形,
根据三角形的外角性质,∠PFP′=∠CPF+∠CP′E′+∠PCP′,
=∠CPF+∠CPE+∠PCP′
=∠EPF+∠PCP′,
∵∠EPF=30°,
∴∠PFP′=30°+60°=90°,
∴△PFP′是直角三角形,
即P′E′2+PF2=PP′2,
∴PE2+PF2=PC2.
故结论①正确,结论②错误.
8
| ||
| x |
∴m=
8
| ||
| 4 |
| 3 |
∴点A的坐标为(4,2
| 3 |
∵点A(4,2
| 3 |
| 3 |
∴
|
解得
|
∴直线解析式为y=
| 3 |
| 3 |
令y=0,则
| 3 |
| 3 |
解得x=2,
∴点C的坐标为(2,0);
(2)y轴上存在点D(0,2
| 3 |
理由如下:设点D的坐标为(0,y),
则CD=
| (2-0)2+(0-y)2 |
AD=
(4-0)2+(2
|
∵CD=DA,
∴
| (2-0)2+(0-y)2 |
(4-0)2+(2
|
两边平方并整理得,4
| 3 |
解得y=2
| 3 |
∴y轴上存在点D(0,2
| 3 |
(3)结论①PE2+PF2=PC2正确.
理由如下:∵点C坐标为(2,0),点E坐标为(0,-2
| 3 |
∴CE=
| CO2+OE2 |
22+(2
|
| OE |
| OC |
2
| ||
| 2 |
| 3 |
∴∠ECO=60°,

又∵点F、C关于y轴对称,
∴FC=2+2=4,
∴FC=CE,
∴△CEF是等边三角形,
如图,把△PCE绕点C顺时针旋转60°得到△P′C′E,连接PP′,
则点E与点F重合,△PP′C为等边三角形,
根据三角形的外角性质,∠PFP′=∠CPF+∠CP′E′+∠PCP′,
=∠CPF+∠CPE+∠PCP′
=∠EPF+∠PCP′,
∵∠EPF=30°,
∴∠PFP′=30°+60°=90°,
∴△PFP′是直角三角形,
即P′E′2+PF2=PP′2,
∴PE2+PF2=PC2.
故结论①正确,结论②错误.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目