题目内容
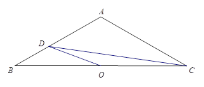
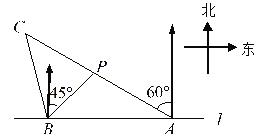
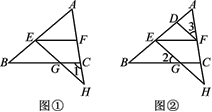
【题目】如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
(1)求∠AED的度数;
(2)当∠EDC满足什么条件时,AE∥DC,证明你的结论.
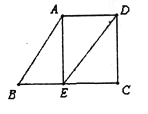
【答案】(1)30°;(2)当∠EDC=30°时, AE∥DC,理由参见解析.
【解析】试题分析:(1)由已知AE⊥BC,可知∠AEC=90°,根据AB∥DE,∠B=60°,得出∠DEC=∠B= 60°(两直线平行,同位角相等),这样∠AED就求出来了;(2)此题是平行线的判定,上题已求出∠AED=30°,利用内错角相等,两直线平行,只要∠EDC=30°就可以判定AE∥DC.
试题解析:(1)∵ AB∥DE, ∴ ∠DEC=∠B= 60°(两直线平行,同位角相等),又∵ BC⊥AE,∴ ∠AEC=90°(垂直定义),所以 ∠AED=90°-60°=30°; (2)由⑴得∠AED=30°,根据内错角相等,两直线平行,∴ ∠AED=∠EDC时 AE∥DC,即当∠EDC=30°时, AE∥DC.

【题目】某校八年级数学实践能力考试选择项目中,选择数据收集项目和数据分析项目的学生比较多。为了解学生数据收集和数据分析的水平情况,进行了抽样调查,过程如下,请补充完整.收集数据:从选择数据收集和数据分析的学生中各随机抽取16人,进行了体育测试,测试成绩(十分制)如下:
数据收集 | 10 | 9.5 | 9.5 | 10 | 8 | 9 | 9.5 | 9 | 7 | 10 | 4 | 5.5 | 10 | 7.9 | 9.5 | 10 |
数据分析 | 9.5 | 9 | 8.5 | 8.5 | 10 | 9.5 | 10 | 8 | 6 | 9.5 | 10 | 9.5 | 9 | 8.5 | 9.5 | 6 |
整理,描述数据:按如下分数段整理,描述这两组样本数据:
|
|
|
| 10 | |
数据收集 | 1 | 1 | 3 | 6 | 5 |
数据分析 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分析数据:两组样本数据的平均数,中位数,众数如下表所示:
项目 | 平均数 | 中位数 | 众数 |
数据收集 | 8.75 | 9.5 | 10 |
数据分析 | 8.81 | 9.25 | 9.5 |
得出结论:
(1)如果全校有480人选择数据收集项目,达到优秀的人数约为________人;
(2)初二年级的井航和凯舟看到上面数据后,井航说:数据分析项目整体水平较高.凯舟说:数据收集项目整体水平较高.你同意________的看法,理由为_______________________.(至少从两个不同的角度说明推断的合理性)