题目内容
如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)旋转.(1)如图2的位置,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
(3)在(2)的条件下,若∠MOB=15°,正方形ABCD的面积为4,求三角形OBM的面积.

分析:(1)根据等腰直角三角形与正方形的性质,可以证明△OBM≌△OFN,根据全等三角形的对应边相等即可求证;
(2)与(1)的证明思路相同,证明△OBM≌△OFN;
(3)求出OQ、BQ的长,解直角三角形,求出MQ,分别求出△OQB和△OQM的面积,即可得出答案.
(2)与(1)的证明思路相同,证明△OBM≌△OFN;
(3)求出OQ、BQ的长,解直角三角形,求出MQ,分别求出△OQB和△OQM的面积,即可得出答案.
解答:(1)BM=FN,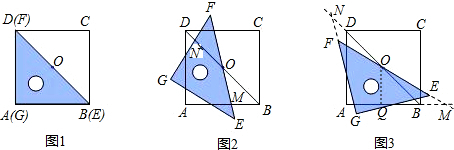
证明:如图2,∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠ABD=∠F=45°,OB=OF,
在△OBM和△OFN中,
∴△OBM≌△OFN(ASA),
∴BM=FN.
(2)BM=FN仍然成立,
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45°,OB=OF,
∴∠MBO=∠NFO=135°,
在△OBM和△OFN中,
∴△OBM≌△OFN(ASA),
∴BM=FN;
(3)解:∵正方形ABCD的面积为4,
∴∠A=90°,AD=AB=2,DO=OB,∠OBQ=45°,
∴由勾股定理得:BD=
=2
,
∴OB=
,
∵∠A=90°,OQ⊥AB,
∴OQ∥AD,
∵DO=BO,
∴AQ=BQ,
∴OQ=
AD=1,BQ=
AB=1,
∵∠OBQ=45°,∠BOM=15°,
∴∠QMO=30°,
∴MQ=
=
,
∴三角形OBM的面积是S△OQM-S△OQB=
×
×1-
×1×1=
.

证明:如图2,∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠ABD=∠F=45°,OB=OF,
在△OBM和△OFN中,
|
∴△OBM≌△OFN(ASA),
∴BM=FN.
(2)BM=FN仍然成立,
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45°,OB=OF,
∴∠MBO=∠NFO=135°,
在△OBM和△OFN中,
|
∴△OBM≌△OFN(ASA),
∴BM=FN;
(3)解:∵正方形ABCD的面积为4,
∴∠A=90°,AD=AB=2,DO=OB,∠OBQ=45°,
∴由勾股定理得:BD=
| 22+22 |
| 2 |
∴OB=
| 2 |
∵∠A=90°,OQ⊥AB,
∴OQ∥AD,
∵DO=BO,
∴AQ=BQ,
∴OQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OBQ=45°,∠BOM=15°,
∴∠QMO=30°,
∴MQ=
| OQ |
| tan30° |
| 3 |
∴三角形OBM的面积是S△OQM-S△OQB=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题主要考查了旋转的性质,全等三角形的性质和判定,勾股定理,解直角三角形的应用,证明两个三角形全等是解题的关键,在解题的过程中要注意两问的联系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

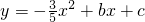 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.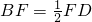 ?(请直接写出答案).
?(请直接写出答案).

 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.